4 tema. Žaidimų teorija ir sąveikos modeliavimas.
1. Pagrindinės žaidimų teorijos sąvokos.
2. Pusiausvyros tipai: Nešo pusiausvyra, Steckelbergo pusiausvyra, Pareto-optimali pusiausvyra, dominuojančių strategijų pusiausvyra.
3. Pagrindiniai žaidimų teorijos modeliai.
Pagrindinės žaidimų teorijos sąvokos.
Matematinių metodų, apimančių žaidimų teoriją, panaudojimas ekonominių procesų analizėje leidžia nustatyti tendencijas ir ryšius, kurie taikant kitus metodus lieka paslėpti ir netgi gauti labai netikėtų rezultatų.
Atminkite, kad žaidimų teorija yra viena iš jauniausių matematikos disciplinų. Jos, kaip savarankiškos matematikos šakos, atsiradimas prasidėjo šeštojo dešimtmečio viduryje, kai buvo išleista garsioji F. Neumanno ir O. Morgensterno monografija „Žaidimų ir ekonominio elgesio teorija“. Žaidimų teorijos ištakos, susijusios su E. Porel (1921) darbais.“
Iki šiol žaidimų teorija virto ištisa matematine sritimi, turtinga įdomių rezultatų ir daugybe praktinių rekomendacijų bei pritaikymų.
Panagrinėkime pagrindines tarpžmonių sąveikos žaidimo modelio prielaidas ir sąvokas.
1. Sąveikaujančių asmenų skaičius yra du. Asmenys vadinami žaidėjais. Žaidėjo samprata leidžia modeliuoti socialinius individo vaidmenis: pardavėjo, pirkėjo, vyro, žmonos ir tt Žaidimas yra supaprastintas dviejų asmenų, turinčių skirtingus ar panašius socialinius vaidmenis, pavyzdžiui, pirkėjo, sąveikos vaizdas. - pardavėjas, pardavėjas - pardavėjas ir kt.
2. Kiekvienas individas turi fiksuotą elgesio variantų rinkinį arba alternatyvas. Skirtingų žaidėjų elgesio parinkčių skaičius gali būti nevienodas.
3. Tarpasmeninė sąveika laikoma įgyvendinta, jei abu žaidėjai vienu metu pasirenka savo elgesio variantus ir elgiasi pagal juos. Vienintelis žmonių sąveikos veiksmas vadinamas žaidimo eiga. Manoma, kad sąveikos veiksmo trukmė yra lygi nuliui.
4. Žaidimo eiga nurodoma dviem sveikaisiais skaičiais – pasirinktu pirmojo žaidėjo elgesio varianto (ėjimo) numeriu ir pasirinktu antrojo žaidėjo elgesio varianto (ėjimo) numeriu. Didžiausias galimas skirtingų ėjimų skaičius žaidime yra lygus pirmojo žaidėjo bendro ėjimų skaičiaus ir bendro antrojo žaidėjo ėjimų skaičiaus sandaugai.
5. Kiekviena asmenų sąveika, arba žaidimo judesys, gauna savo eilės numerį: 1, 2, 3 ir t.t. Nereikėtų painioti sąvokų „žaidimo judėjimas“ (skaičių pora) ir „žaidimo judėjimo skaičius“ (vienas skaičius). Manoma, kad sąveika vyksta reguliariai reguliariais intervalais, todėl žaidimo eilės skaičius rodo laiką, kurį tam tikri asmenys bendrauja tarpusavyje.
6. Kiekvienas žaidėjas siekia pasiekti maksimalią tam tikro tikslo rodiklio reikšmę, kuris vadinamas naudingumu, arba laimėjimu. Taigi žaidėjas turi „ekonominio žmogaus“ bruožus. Žaidėjo atlyginimas gali būti teigiamas arba neigiamas. Neigiamas pelnas taip pat vadinamas nuostoliu.
7. Kiekvienas žaidimo ėjimas (žaidėjų pasirinkta alternatyvų pora) atitinka vieną žaidėjo laimėjimų porą. Žaidėjų laimėjimų priklausomybę nuo pasirinktų ėjimų apibūdina žaidimo matrica, arba išmokėjimo matrica. Šios matricos eilutės atitinka pirmojo žaidėjo alternatyvas (ėjimus), o stulpeliai – antrojo žaidėjo alternatyvas (ėjimus). Žaidimo matricos elementai yra laimėjimų poros, atitinkančios atitinkamą eilutę ir stulpelį (žaidėjo judesius). Pirmojo žaidėjo (pirmasis skaičius žaidimo matricos langelyje) laimėjimas priklauso ne tik nuo jo ėjimo (eilės numeris), bet ir nuo antrojo žaidėjo ėjimo (stulpelio numeris). Todėl prieš įgyvendindamas sąveiką asmuo nežino tikslios savo naudos sumos. Kitaip tariant, žaidėjo elgesys pasirenkamas neapibrėžtumo sąlygomis, t.y. žaidėjas turi „institucinio asmens“ bruožus.
8. Žaidėjo strategija yra įprastas elgesio modelis, kuriuo žaidėjas vadovaujasi pasirinkdamas alternatyvų elgesį per tam tikrą laikotarpį. Žaidėjo strategiją lemia visų įmanomų elgesio variantų pasirinkimo tikimybės (arba dažniai). Kitaip tariant, žaidėjo strategija yra vektorius, kurio koordinačių skaičius yra lygus iš viso galimos alternatyvos ir i-oji koordinatė lygi tikimybei (dažniui) pasirinkimas i-tas alternatyvas. Akivaizdu, kad visų tam tikro vektoriaus koordinačių reikšmių suma yra lygi vienetui.
Jei žaidėjas pasirenka tik vieną elgesio variantą per nagrinėjamą laikotarpį, tada iškviečiama žaidėjo strategija švarus.
Visos atitinkamo grynojo strategijos vektoriaus koordinatės yra lygios nuliui, išskyrus vieną, kuri yra lygi vienetui.
Strategija, kuri nėra gryna, vadinama sumaišytas.
Šiuo atveju žaidėjo strategijos vektorius turi bent dvi koordinates, kurios skiriasi nuo nulio. Jie reaguoja į aktyvaus elgesio parinktis. Žaidėjas, besilaikantis mišrios strategijos, kaitalioja aktyvius elgesio variantus pagal pasirinktas pasirinkimo tikimybes (dažnius). Toliau, dėl pateikimo paprastumo, manysime, kad žaidėjas visada vadovaujasi tam tikra strategija, t.
Instituciniam asmeniui būdingas jo elgesio kintamumas, kuris priklauso nuo jo vidinė būsena, gyvenimo patirtis, išorinė socialinė aplinka ir kt. Žaidimo požiūrio į institucijų tyrimą rėmuose ši institucinio asmens savybė išreiškiama galimybe žaidėjui keisti savo strategiją. Jei tarp žaidėjo strategijų visada būtų objektyviai geresnė, tada jis visada jos laikytųsi ir strategijos keitimas būtų beprasmis. Bet į Tikras gyvenimasžmogus dažniausiai svarsto kelias elgesio strategijas. Iš jų neįmanoma objektyviai išskirti geriausių. Žaidybinis tarpžmonių sąveikos modelis leidžia ištirti šią institucinio elgesio ypatybę, nes jis apima daugybę elgesio strategijų, kurios viena kitos nepaneigia ir atspindi įvairius institucinio asmens elgesio aspektus. Pažvelkime į šiuos elgesio modelius.
Žaidimo matrica
| Pirmasis žaidėjas | Antras žaidėjas | ||
| 6; 15 | 2; 13 | 3; 11 | |
| 1; 10 | 5; 14 | 4; 12 | |
| 4; 12 | 4; 13 | 3; 13 |
Išskirti solidariai Ir nesolidarumo elgesio strategijos. Pirmieji labiausiai būdingi „instituciniam žmogui“, o antrieji - „ekonominiam žmogui“.
Nesolidarumas elgesio strategijoms būdinga tai, kad individas savarankiškai pasirenka savo elgesį, tuo tarpu jis arba visiškai neatsižvelgia į kito individo elgesį, arba, remdamasis turima patirtimi, daro prielaidą galimas variantas jo elgesys.
Pagrindiniai nesolidarumo elgesio tipai yra šie: neracionalus, atsargus, optimizavimas, deviantas Ir naujoviškas.
1) Neracionalus elgesys. Dvi pirmojo žaidėjo strategijas pažymėkime atitinkamai A ir B. Sakoma, kad strategija A yra dominuojanti strategijos B atžvilgiu, jei po bet kurio antrojo žaidėjo ėjimo pirmojo žaidėjo, atitinkančio strategiją A, laimėjimas yra didesnis nei jo laimėjimas, atitinkantis strategiją B. Taigi strategija B yra objektyviai blogesnė Pagarba strategijai A.
Jei žaidėjas visada gali laisvai pasirinkti strategiją A, tai strategija B apskritai neturėtų būti pasirinkta. Jei vis dėlto strategiją B pasirenka pirmasis žaidėjas, tai jo elgesys šiuo atveju vadinamas neracionaliu. Norint nustatyti neracionalų žaidėjo elgesį, pakanka išanalizuoti jo išmokėjimo matricą: kito žaidėjo išmokėjimo matrica nenaudojama.
Atkreipkite dėmesį, kad terminas „neracionalus elgesys“ yra pasiskolintas iš neoklasikinės teorijos. Tai tik reiškia, kad šios strategijos pasirinkimas tikrai nėra pats geriausias situacijoje, kai abu žaidėjai yra antagoniškoje konfrontacijoje, būdingoje „ekonominiam žmogui“. Tačiau „instituciniam asmeniui“, kuris užmezga tarpasmeninę sąveiką su kitais žmonėmis, neracionalus elgesys yra ne tik įmanomas, bet ir gali pasirodyti pats protingiausias veiksmas. To pavyzdys yra žaidimas „Kalinių dilema“.
2) Atsargus elgesys. „Institucinis žmogus“, skirtingai nei „ekonominis žmogus“, nėra absoliučiai racionalus, t.y. jis ne visada pasirenka geriausią elgesį, kuris maksimaliai padidina naudą. Ribotas „institucinio asmens“ racionalumas išreiškiamas jo nesugebėjimu pasirinkti geriausio veikimo būdo dėl daugybės alternatyvų, sudėtingo optimalios alternatyvos nustatymo algoritmo, riboto sprendimų priėmimo laiko ir kt. Tuo pačiu metu riboto racionalumo samprata daro prielaidą, kad, atsižvelgiant į visus pasirinkimo sudėtingumus, žmogus gali pasirinkti gana gerą alternatyvą.
Žaidimo požiūriu į institucijų tyrimą ribotą individo racionalumą iliustruoja kruopštus žaidėjo elgesys.
Atsargaus elgesio strategija- tai žaidėjo strategija, kuri garantuoja jam tam tikrą laimėjimo sumą, nepriklausomai nuo kito žaidėjo pasirinkimo (ėjimo). Atsargioji strategija dar vadinama maximin, nes ji apskaičiuojama ieškant didžiausios reikšmės iš kelių minimalių verčių.
Pirmojo žaidėjo atsargumo strategija apibrėžiama taip. Kiekvienoje jo laimėjimo matricos eilutėje randamas minimalus elementas, o tada iš tokių minimalių elementų parenkamas pirmojo žaidėjo maksimalus arba maksimumas. Žaidimo matricos eilutė, kurioje yra pirmojo žaidėjo maksimumas, atitinka jo atsargią strategiją. Panaši ir antrojo žaidėjo atsargumo strategija. Kiekviename jo laimėjimų matricos stulpelyje randamas minimalus elementas, o tada iš tokių minimalių elementų nustatomas maksimalus elementas. Žaidimo matricos stulpelis, kuriame yra antrojo žaidėjo maksimumas, atitinka jo atsargią strategiją. Kiekvienas žaidėjas gali turėti kelias atsargias strategijas, tačiau jos visos turi tą pačią reikšmę maxima (aukštas-žemas strategija), arba garantuotus laimėjimus. Atsargios strategijos egzistuoja bet kuriame matricos žaidime. Norint nustatyti žaidėjo atsargią strategiją, pakanka išanalizuoti jo išmokėjimo matricą, nenaudojant kito žaidėjo išmokėjimo matricos. Ši savybė būdinga neracionaliam ir atsargiam elgesiui.
3) Elgesio optimizavimas. Ekonominėje praktikoje dažnai susiklosto situacijos, kai ūkio subjektai (pavyzdžiui, pardavėjas ir nuolatinis pirkėjas), ilgai bendraudami vienas su kitu, randa abiem pusėms tinkamas elgesio strategijas, todėl jas naudoja „. žaidėjai“ ilgą laiką. Žaidimo požiūriu į institucijų tyrimą aprašyta situacija modeliuojama naudojant pusiausvyros strategijų sampratą. Tokių strategijų porai būdinga tokia savybė: jei pirmasis žaidėjas nukrypsta nuo savo pusiausvyros strategijos (pasirenka kitą), o antrasis toliau laikosi savo pusiausvyros strategijos, tada pirmasis žaidėjas patiria žalą mažėjimo forma. laimėjimų suma. Pusiausvyros strategijų porą atitinkanti žaidimo matricos ląstelė, esanti eilutės ir stulpelio sankirtoje, vadinama pusiausvyros tašku. Žaidimo matrica gali turėti kelis pusiausvyros taškus arba gali jų visai neturėti.
Žaidėjo elgesys, laikantis pusiausvyros strategijos, vadinamas optimizavimu ( Minimax elgesys arba minmax strategija).
Tai skiriasi nuo elgesio maksimizavimo. Pirma, žaidėjo pusiausvyros laimėjimas nėra didžiausias iš visų galimų išmokėjimų. Jis atitinka ne globalų maksimumą, o lokalųjį optimalumą, todėl globalus funkcijos maksimumas, apibrėžtas skaitiniame intervale, viršija kiekvieną jos lokalų maksimumą. Antra, vienam žaidėjui vadovaujantis pusiausvyros strategija, vietinis maksimumas pasiekiamas tik tada, kai kitas žaidėjas laikosi pusiausvyros strategijos. Jei antrasis žaidėjas nukrypsta nuo pusiausvyros strategijos, tai pirmasis žaidėjas toliau naudodamas pusiausvyros strategiją nesuteiks jam maksimalaus efekto.
Pusiausvyros strategijos nustatomos pagal šią taisyklę: žaidimo matricos ląstelė laikoma pusiausvyra, jei pirmojo žaidėjo atitinkama išmoka yra didžiausia stulpelyje, o antrojo žaidėjo atitinkama išmoka yra didžiausia eilutėje. Taigi, pusiausvyros strategijų paieškos algoritmas naudoja abiejų žaidėjų atsipirkimo matricas, o ne vieno iš jų, kaip neracionalaus ir atsargaus elgesio atvejais.
4) Deviantinis elgesys. Pusiausvyros strategijos, kaip pagrindinės elgesio normos, institucionalizavimas atsiranda dėl to, kad asmuo apibendrina savo tarpasmeninės sąveikos patirtį, įskaitant deviantinio elgesio patirtį. Asmens suvokimas apie neigiamas tokio elgesio pasekmes, pagrįstas nepusiausvyros alternatyvų pasirinkimu, yra lemiamas argumentas renkantis optimizuojančią elgesio strategiją. Taigi deviantinis elgesys yra neatsiejama „institucinio asmens“ gyvenimo patirties dalis, tarnaujanti kaip empirinis elgsenos optimizavimo pagrindimas. Deviantinio elgesio patirtis suteikia žmogui pasitikėjimo, kad kitas žaidimo dalyvis visada laikysis pusiausvyros strategijos. Taigi tokia patirtis yra kito žaidėjo elgesio racionalumo ir būsimos sąveikos su juo nuspėjamumo įrodymas.
5) Inovatyvus elgesys. Aukščiau buvo nagrinėjamas deviantinis elgesys, kurio pagrindinis tikslas yra empiriškai pagrįsti ir įtvirtinti pirminę pusiausvyros strategiją. Tačiau nukrypimo nuo pusiausvyros strategijos tikslas gali būti iš esmės skirtingas. Inovatyvus elgesys – tai sistemingas nukrypimas nuo įprastos pusiausvyros strategijos, siekiant rasti kitą pusiausvyros būseną, kuri novatoriui būtų naudingesnė.
Tarpžmonių sąveikų žaidimo modelio rėmuose novatoriško elgesio tikslas gali būti pasiektas, jei žaidimo matrica turi skirtingą pusiausvyros tašką, kuriame novatoriaus žaidėjo atsipirkimas yra didesnis nei pradinėje pusiausvyros būsenoje. Jei tokio taško nėra, novatoriškas elgesys greičiausiai bus pasmerktas nesėkmei, o novatorius grįš prie pradinės pusiausvyros strategijos. Be to, jo nuostoliai dėl inovacijų eksperimento bus lygūs bendram nuokrypio efektui per visą eksperimento laikotarpį.
Realiame gyvenime bendraujantys asmenys dažnai sutinka ateityje laikytis tam tikrų elgesio strategijų. Tokiu atveju vadinamas žaidėjų elgesys solidariai.
Pagrindinės solidaraus elgesio priežastys:
a) solidaraus elgesio nauda abiem žaidėjams. Žaidimo sąveikos modelio rėmuose šią situaciją iliustruoja žaidimo matrica, kurios vienoje ląstelėje abiejų žaidėjų išmokos yra didžiausios, tačiau kartu ji nėra pusiausvyra ir neatitinka poros atsargiųjų. žaidėjų strategijos. Vargu ar pasirinks šią ląstelę atitinkančias strategijas žaidėjai, įgyvendinantys nesolidarumo elgesio modelius. Bet jei žaidėjai susitars dėl tinkamų solidarių strategijų pasirinkimo, vėliau jiems bus nenaudinga pažeisti susitarimą ir tai bus vykdoma automatiškai;
b) solidaraus elgesio etika dažnai tarnauja kaip „vidinis“ mechanizmas, užtikrinantis susitarimo laikymąsi. Moralinės išlaidos socialinio pasmerkimo pavidalu, kurias patirs asmuo, pažeisdamas susitarimą, jam gali būti svarbesnės nei šiuo atveju pasiektas laimėjimo padidėjimas. Etinis veiksnys vaidina svarbų vaidmenį „institucinio žmogaus“ elgesyje, tačiau tarpžmonių sąveikos žaidimo modelyje į jį faktiškai neatsižvelgiama;
c) solidarumo vykdymas yra „išorinis“ mechanizmas, užtikrinantis susitarimo laikymąsi. Šis institucinio elgesio veiksnys taip pat nėra tinkamai atspindėtas sąveikos žaidimo modelyje.
Pusiausvyros tipai: Nešo pusiausvyra, Steckelbergo pusiausvyra, Pareto-optimali pusiausvyra, dominuojančių strategijų pusiausvyra.
Kiekvienoje sąveikoje gali egzistuoti skirtingų tipų pusiausvyra: dominuojančios strategijos pusiausvyra, Nash pusiausvyra, Stackelbergo pusiausvyra ir Pareto pusiausvyra. Dominuojanti strategija – tai veiksmų planas, suteikiantis dalyviui maksimalų naudingumą, nepaisant kito dalyvio veiksmų. Atitinkamai, dominuojančių strategijų pusiausvyra bus abiejų žaidimo dalyvių dominuojančių strategijų sankirta. Nash equilibrium – tai situacija, kai kiekvieno žaidėjo strategija yra geriausias atsakas į kito žaidėjo veiksmus. Kitaip tariant, ši pusiausvyra suteikia žaidėjui didžiausią naudingumą, priklausomai nuo kito žaidėjo veiksmų. Stackelbergo pusiausvyra atsiranda tada, kai žaidimo dalyviai priima sprendimus laiko delsa: vienas iš jų priima sprendimus jau žinodamas, ką padarė kitas. Taigi Stackelbergo pusiausvyra atitinka maksimalų žaidėjų naudingumą, kai jie priima sprendimus ne vienu metu. Skirtingai nuo dominuojančių strategijų pusiausvyros ir Nešo pusiausvyros, tokio tipo pusiausvyra visada egzistuoja. Galiausiai Pareto pusiausvyra egzistuoja su sąlyga, kad neįmanoma vienu metu padidinti abiejų žaidėjų naudingumo. Panagrinėkime vieną visų keturių tipų pusiausvyros paieškos technologijos pavyzdį.
Dominuojanti strategija- veiksmų planas, suteikiantis dalyviui maksimalų naudingumą, neatsižvelgiant į kito dalyvio veiksmus.
Nešo pusiausvyra- situacija, kai nė vienas iš žaidėjų negali vienašališkai padidinti savo laimėjimo, pakeisdamas veiksmų planą.
Stackelbergo pusiausvyra- situacija, kai nė vienas žaidėjas negali vienašališkai padidinti savo laimėjimo, o sprendimus pirmiausia priima vienas žaidėjas, o antrasis tampa žinomas.
Pareto pusiausvyra- situacija, kai neįmanoma pagerinti vieno iš žaidėjų padėties nepabloginant kito padėties ir nesumažinus žaidėjų bendro laimėjimo.
Tegul įmonė A siekia sulaužyti įmonės B monopolį produkcijos srityje konkretus produktas. Įmonė A nusprendžia, ar ji turėtų patekti į rinką, o įmonė B nusprendžia, ar ji turėtų sumažinti gamybą, jei A nuspręs įeiti. Jei įmonėje B nuolat gaminama produkcija, abi įmonės yra pralaimėjusios, tačiau jei įmonė B nusprendžia sumažinti produkciją, ji „dalijasi“ savo pelnu su A.
Dominuojančių strategijų pusiausvyra. Įmonė A lygina savo pelną pagal abu scenarijus (-3 ir O, jei B nusprendžia pradėti kainų karą) ir (4 ir 0, jei B nusprendžia sumažinti gamybą). Ji neturi strategijos, kuri užtikrintų maksimalų pelną, nepaisant B veiksmų: 0 > -3 => „neįeiti į rinką“, jei B palieka produkciją tame pačiame lygyje, 4 > 0 => „įeiti“, jei B sumažina produkciją (žr. kietos rodyklės). Nors įmonė A neturi dominuojančios strategijos, įmonė B turi. Ji suinteresuota sumažinti našumą, nepaisant A veiksmų (4 > -2, 10 = 10, žr. punktyrines rodykles). Vadinasi, nėra dominuojančių strategijų pusiausvyros.
Nešo pusiausvyra. Geriausias firmos A atsakas į firmos B sprendimą palikti produkciją nepakitusią yra neįeiti, o į sprendimą sumažinti gamybą – įeiti. Geriausias firmos B atsakas į firmos A sprendimą įeiti į rinką yra produkcijos mažinimas, nusprendus neįeiti, abi strategijos yra lygiavertės. Todėl dvi Našo pusiausvyros (A, A2) yra taškuose (4, 4) ir (0, 10) – A įeina, o B sumažina išėjimą, arba A neįeina, o B nesumažina išėjimo. Tai gana lengva patikrinti, nes šiais momentais nė vienas iš dalyvių nėra suinteresuotas keisti savo strategiją.
Stackelbergo pusiausvyra. Tarkime, kad firma A priima pirmąjį sprendimą. Jei ji pasirenka įeiti į rinką, ji galiausiai atsidurs taške (4, 4): firmos B pasirinkimas šioje situacijoje yra aiškus, 4 > -2. Jei ji nuspręs susilaikyti nuo įėjimo į rinką, rezultatas bus du taškai (0, 10): Įmonės B pirmenybės leidžia pasirinkti abu variantus. Žinodama tai, įmonė A maksimaliai padidina savo pelną taškuose (4, 4) ir (0, 10), lygindama 4 ir 0. Pirmenybės yra vienareikšmės, o pirmoji Stackelbergo pusiausvyra StA bus taške (4, 4). Panašiai Stackelbergo pusiausvyros StB, kai įmonė B nusprendžia pirmoji, bus taške (0, 10).
Pareto pusiausvyra. Norėdami nustatyti Pareto optimalumą, turime paeiliui išbandyti visus keturis žaidimo rezultatus, atsakydami į klausimą: „Ar perėjimas prie kito žaidimo rezultato padidina abiejų dalyvių naudingumą vienu metu? Pavyzdžiui, iš rezultato (-3, -2) galime pereiti prie bet kurio kito rezultato, atitinkančio nurodytą sąlygą. Tik iš rezultato (4, 4) negalime judėti toliau nesumažindami nė vieno žaidėjo naudingumo, tai bus Pareto pusiausvyra, R.
Pradėdami spręsti problemą, pirmiausia turite nustatyti nagrinėjamos sistemos (ypač mechanizmo) laisvės laipsnių skaičių pagal nepriklausomų galimų sistemos judesių ar koordinačių skaičių.
Plokščiuose mechanizmuose laisvės laipsnių skaičių galima praktiškai nustatyti taip. Įsivaizduokime, kad mechanizmas juda. Jei, sustabdę kurios nors vienos grandies transliacinį ar sukamąjį judėjimą, kartu sustabdome visą mechanizmą, tai jis turi vieną laisvės laipsnį. Jei po šios mechanizmo dalies gali judėti toliau, bet sustabdžius kitos jungties judėjimą, mechanizmas sustoja, tada jis turi du laisvės laipsnius ir tt Panašiai, jei mechanizmo padėtį nustatome kai kuriais koordinatės ir kai ji yra pastovi, mechanizmas negali judėti - jis turi vieną laisvės laipsnį. Jei po to dalis mechanizmo gali judėti, tada pasirenkama antroji koordinatė ir pan.
Norint išspręsti problemą geometriniu metodu, kai sistema turi vieną laisvės laipsnį, reikia: 1) pavaizduoti visas sistemą veikiančias aktyviąsias jėgas; 2) informuoti sistemą apie galimą poslinkį ir brėžinyje parodyti elementarius jėgų ar kampų taikymo taškų poslinkius 69, elementarius kūnų, kuriuos veikia jėgos, poslinkius (elementariesiems poslinkiams brėžinyje nurodysime jų modulius, kurie tiesiogiai patekti į pusiausvyros sąlygas); 3) apskaičiuokite elementarų visų aktyviųjų jėgų darbą esant tam tikram poslinkiui, naudodami formules:
ir sukurti sąlygą (99); 4) nustatyti santykį tarp dydžių, įtrauktų į lygybę (99), ir išreikšti šiuos dydžius per bet kurį, ką visada galima padaryti vieno laisvės laipsnio sistemai.
Pakeitę visus lygybės (99) dydžius po vieną, gauname lygtį, iš kurios galime rasti užduotyje ieškomą kiekį arba priklausomybę.
Priklausomybes tarp galima rasti: a) iš atitinkamų geometrinių ryšių (164, 169 uždaviniai); b) iš kinematinių santykių, atsižvelgiant į tai, kad sistema juda, ir tam tikroje sistemos padėtyje nustatant priklausomybes tarp atitinkamų sistemos taškų arba kūnų tiesinių arba kampinių greičių, ir tada darant prielaidą, kad tai tiesa, kadangi tikrieji judesiai, gauti taškų ar kūnų per laiką, kurį dt bus ties stacionariais ryšiais, yra vieni iš galimų (kitaip čia galime iš karto laikyti priklausomybes tarp galimų judesių tokiomis pat kaip ir tarp atitinkamų greičių, žr. uždavinius 165 , 166 ir kt.).
Sistemai su keliais laisvės laipsniais problema gali būti išspręsta sukonstruojant sąlygą (99) kiekvienam iš nepriklausomų galimų sistemos judesių ir transformuojant ją tokiu pačiu būdu. Dėl to sistema turės tiek pusiausvyros sąlygų, kiek ji turės laisvės laipsnių. Kitas sprendimo būdas, leidžiantis gauti tuos pačius rezultatus, aprašytas 144 straipsnyje.
Taikant analitinio skaičiavimo metodą, pusiausvyros sąlyga rašoma forma (100). Norėdami tai padaryti, pasirinkite koordinačių ašis, susijusias su kūnu, kuris nejuda galimų sistemos judesių metu. Tada apskaičiuojamos visų aktyviųjų jėgų projekcijos į pasirinktas ašis ir šių jėgų taikymo taškų koordinatės, išreiškiančios visas koordinates per kokį nors parametrą (pavyzdžiui, kampą). Po to dydžiai nustatomi diferencijuojant koordinates šio parametro atžvilgiu.
Jei neįmanoma išreikšti visų koordinačių vienu parametru vienu metu, turite įvesti kelis parametrus ir nustatyti ryšį tarp jų.
Pabaigoje pažymėkime, kad sąlygos (99) arba (100) gali būti naudojamos problemoms spręsti esant trinčiai, įskaitant trinties jėgą tarp aktyviųjų jėgų. Lygiai taip pat galima rasti ir jungčių reakcijas, jei, atmetus ryšį, pakeisti ją atitinkama reakcija, pastarąją įtraukti į aktyviųjų jėgų skaičių ir atsižvelgti į tai, kad atmetus ryšį, sistema turi naują laisvės laipsnį.
Uždavinys 164. Mechanizme, parodytame pav. 354, raskite ryšį tarp jėgų P ir Q pusiausvyroje.
Sprendimas: sistema turi vieną laisvės laipsnį. Jei pasakysite sistemai galimą judėjimą, tada visos strypų suformuotų lygiagretainių įstrižainės pailgės tiek pat. Tada .
Sudarę (99) lygtį, gauname:
kur . Rezultatas labai paprastas.
165 uždavinys. Rąsto svoris yra Q, kiekvieno iš dviejų cilindrinių ritinėlių, ant kurių jis uždėtas, svoris yra P. Nustatykite, kokia jėga F turi būti veikiamas rąstas, kad jis išlaikytų pusiausvyrą nuožulnioje plokštumoje duotas pasvirimo kampas a (355 pav.). Ritinėlių trintis į plokštumą ir rąstą užtikrina, kad nebūtų slydimo.
Sprendimas. Jei nepaisysime pasipriešinimo riedėjimui, tada ritinėlių plokštuma bus ideali jungtis. Riedant neslystant sistema turi vieną laisvės laipsnį. Informuodami sistemą apie galimą judėjimą, gauname pagal sąlygą (99)
kur galimas rąsto judėjimas, sutampantis su taško B judėjimu.
Lietimo taškas K yra momentinis volo greičio centras. Todėl, jei apsvarstysime , Pakeitę šią reikšmę į ankstesnę lygtį, pagaliau rasime
![]()
Užduotis 166. Raskite ryšį tarp momento M poros, veikiančios švaistiklio-slankiklio mechanizmo švaistiklį (356 pav.) ir slėgio jėgos P stūmoklį pusiausvyros būsenoje, jei


Sprendimas. Mechanizmas turi vieną laisvės laipsnį. Iš pusiausvyros sąlygos (99), jei ją įdėsime, gausime:
Sprendimas yra susijęs su ryšio tarp Ši kinematinė problema išspręsta anksčiau (žr. § 57, 63 uždavinį). Naudodami ten gautą rezultatą, randame
![]()
167 uždavinys. 83 užduotyje nagrinėjamai pavarų dėžei (žr. § 70) raskite ryšį tarp pavaros velenui A taikomo sukimo momento ir varomojo veleno B pasipriešinimo momento, kai abu velenai sukasi tolygiai.
Sprendimas. Tolygiai sukantis, santykis tarp bus toks pat kaip ir esant pusiausvyrai. Todėl pagal sąlygą (99), jei įdėsime, bus:
Iš čia, naudodami 83 uždavinyje gautą rezultatą, randame
168 uždavinys. Kėlimo mechanizme, kurio dalys paslėptos dėžėje K (357 pav.), jėgų P ir Q rašto ryšys, jei žinoma, kad su kiekvienu rankenos pasukimu varžtas D pasislenka tam tikru dydžiu.
Sprendimas. Sudarę pusiausvyros sąlygą (99), gauname
Daroma prielaida, kad vienodai sukant rankeną, tada taip pat tolygiai atsukamas viit
Pakeitę šią reikšmę į ankstesnę lygybę, randame
Atkreipkite dėmesį, kad šios paprastos problemos iš viso nepavyko išspręsti geometrinės statikos metodais, nes mechanizmo detalės nėra žinomos.
Išspręstas uždavinys parodo, kokios (iš esmės) yra taikomo metodo galimybės. Tačiau atliekant konkretų tokio mechanizmo inžinerinį skaičiavimą, žinoma, reikės atsižvelgti į trintį tarp jo dalių, dėl kurių turėsite žinoti, koks yra mechanizmas.
169 uždavinys. Sija, susidedanti iš dviejų sijų, sujungtų vyriais C, neša apkrovą P (358 pav., a). Sijos matmenys ir atramų vieta nurodyti brėžinyje. Nustatykite slėgio jėgą atramai B, kurią sukelia tam tikra apkrova.


Sprendimas. Atramą B išmetame ir pakeičiame reakcija N in, skaičiais lygia norimai slėgio jėgai (358 pav., b). Informavę sistemą apie galimą judėjimą (dabar ji turi vieną laisvės laipsnį), sudarome sąlygą (99)
Randame ryšį tarp proporcijų:
Vadinasi,
![]()
Taikant geometrinės statikos metodą, sprendimas būtų buvęs ilgesnis (reikėjo atsižvelgti į pluošto dalių pusiausvyrą ir įvesti papildomas kitų jungčių reakcijas, o vėliau šias reakcijas neįtraukti iš gautos pusiausvyros lygčių sistemos) .
170 uždavinys. Horizontali sija 1 su svarmeniu, pritvirtintu taške A vyriais (359 pav.), vyriais B sujungta su sija 2 su svarmeniu C gale, sija remiasi į horizontalias grindis, sudarydama kampą a su tai. Nustatykite, kokiai vertei sijos trinties jėga grindyse bus pusiausvyra.


Sprendimas. Pavaizduojame sistemą veikiančias jėgas ir trinties jėgą F, įtraukiant ją į aktyviąsias jėgas; šiuo atveju jėgą išskaidome į dvi dedamąsias, kurių kiekviena yra lygi ir taikoma taškuose B ir C (atkreipkite dėmesį į šią techniką, kuri žymiai palengvina galimo darbo skaičiavimą).
Sudarę pusiausvyros sąlygą (99) ir atsižvelgdami į formules (101), gauname žymintį
Bet, pagal analogiją su teorema apie dviejų kūno taškų greičių projekcijas, Kur . Tada ir galiausiai
Atkreipkite dėmesį, kad naudojant geometrinės statikos metodus šiame uždavinyje neįmanoma sukurti tik vienos lygties, iš kurios iš karto būtų galima rasti F.
171 uždavinys. Planetiniame mechanizme su diferencine pavara (žr. § 70) ant ašies A nepriklausomai viena nuo kitos sumontuota 1 krumpliaratis su spinduliu ir švaistiklis AB, kuri neša 2 krumpliaračio su spinduliu ašį B (360 pav.). Alkūninį mechanizmą veikia sukimo momentas M, o pavaras 1 ir 2 – pasipriešinimo momentai. Raskite vertes, kai mechanizmas yra pusiausvyroje.
Pagrindiniai dualumo teorijos apibrėžimai.Kiekviena linijinio programavimo problema gali būti susieta su kita linijinio programavimo problema. Išsprendus vieną iš jų, automatiškai išsprendžiama kita problema. Tokios problemos vadinamos abipusiai dvejopomis. Parodykime, kaip panaudoti duotąją problemą (vadinsime ją originalia) jos dualui sukurti.
Apsvarstykite planuojamos gamybos problemą.
F = 3 X 1 + 5X 2 + 4X 3 + 5X 4 → maks.
5x1 +0,4x2 +2x3 +0,5x4 ≤400
5x 2 +x 3 +x 4 ≤300
x 1 +x 3 +x 4 ≤100
x 1 ≥0, x 2 ≥0, x 3 ≥0, x 4 ≥0
Bendrosios dvigubos problemos sudarymo taisyklės:
| Tiesiai | Dvigubas |
| Tikslinė funkcija (maks.) | Dešinė apribojimų pusė |
| Dešinė apribojimų pusė | Objektyvi funkcija (min.) |
| A – apribojimo matrica | A T – apribojimo matrica |
| i-asis apribojimas: ≤ 0, (≥ 0) | Kintamasis y i ≥ 0, (≤ 0) |
| i-asis apribojimas: = 0 | Kintamasis y i ≠ 0 |
| Kintamasis x j ≥ 0 (≤ 0) | |
| Kintamasis x j ≠ 0 | j-asis apribojimas: = 0 |
| Tiesiai | Dvigubas |
| Objektyvi funkcija (min.) | Dešinė apribojimų pusė |
| Dešinė apribojimų pusė | Tikslinė funkcija (maks.) |
| A – apribojimo matrica | A T – apribojimo matrica |
| i-asis apribojimas: ≥ 0, (≤ 0) | Kintamasis y i ≥ 0, (≤ 0) |
| i-asis apribojimas: = 0 | Kintamasis y i ≠ 0 |
| Kintamasis x j ≥ 0 (≤ 0) | j-asis apribojimas: ≤ 0 (≥ 0) |
| Kintamasis x j ≠ 0 | j-asis apribojimas: = 0 |
Sukurkime jos dvigubą problemą pagal šias taisykles.
- Kintamųjų skaičius dviguboje užduotyje yra lygus nelygybių skaičiui pradinėje užduotyje.
- Dvigubo uždavinio koeficientų matrica perkeliama į pradinės problemos koeficientų matricą.
- Pradinio uždavinio laisvųjų terminų stulpelis yra dvigubos tikslo funkcijos koeficientų eilutė. Tikslinė funkcija vienoje problemoje yra maksimaliai padidinta, o kitoje – sumažinama.
- Pirminės problemos kintamųjų neneigiamumo sąlygos atitinka dualo nelygybes-suvaržymus, nukreiptus kita kryptimi. Ir atvirkščiai, nelygybės-suvaržymai originale atitinka dualo neneigiamumo sąlygas.
Atkreipkite dėmesį, kad I užduoties matricos eilutės yra II užduoties matricos stulpeliai. Todėl II uždavinio kintamųjų y i koeficientai atitinkamai yra I uždavinio i-osios nelygybės koeficientai.
Gautas modelis yra ekonominis-matematinis problemos modelis, susietas su tiesiogine problema.
Rodyklėmis sujungtos nelygybės bus skambučio konjugatas.
Prasminga dvigubos problemos formuluotė: suraskite tokią išteklių kainų (įverčių) rinkinį Y = (y 1, y 2 ..., y m), kuriai esant bendros išteklių sąnaudos bus minimalios, su sąlyga, kad išteklių sąnaudos kiekvienos rūšies gamyboje produkcijos bus ne mažesnė už pelną (pajamas) iš šių produktų pardavimo.
Išteklių kainos y 1, y 2 ..., y m ekonominėje literatūroje gavo įvairius pavadinimus: apskaitinė, numanoma, šešėlinė. Šių pavadinimų reikšmė yra ta, kad tai yra sąlyginės, „netikros“ kainos. Priešingai nei „išorinės“ produktų kainos c 1, c 2 ..., c n, paprastai žinomos prieš pradedant gamybą, išteklių kainos c 1, c 2 ..., c n yra vidinės, nes jos nėra nustatomi iš išorės, o nustatomi tiesiogiai sprendžiant problemą, todėl jie dažniau vadinami išteklių įvertinimais.
Ryšys tarp tiesioginių ir dvigubų problemų visų pirma slypi tame, kad vienos iš jų sprendimas gali būti gaunamas tiesiogiai sprendžiant kitą.
Dualumo teoremos
Dvilypumas yra pagrindinė linijinio programavimo teorijos sąvoka. Pagrindiniai dualumo teorijos rezultatai yra dviejose teoremose, vadinamose dualumo teoremomis.Pirmoji dvilypumo teorema.
Jei viena iš dviejų I ir II uždavinių poros yra sprendžiama, tai kita yra išsprendžiama, o objektyvių funkcijų reikšmės optimaliuose planuose sutampa, F(x*) = G(y*), kur x *, y * yra optimalūs I ir II uždavinių sprendimai
Antroji dvilypumo teorema.
Planai x * ir y * yra optimalūs I ir II uždaviniuose tada ir tik tada, kai juos pakeičiant atitinkamai I ir II uždavinių suvaržymų sistema, bent viena iš bet kurios konjuguotų nelygybių poros virsta lygybe.
Tai pamatinė dvilypumo teorema. Kitaip tariant, jei x * ir y * yra įmanomi tiesioginių ir dvigubų uždavinių sprendimai ir jei c T x * = b T y *, tai x * ir y * yra optimalūs dvigubų uždavinių poros sprendimai.
Trečioji dvilypumo teorema. Kintamųjų y i reikšmės optimaliame dvigubos problemos sprendime yra apribojimų sistemos laisvųjų terminų b i - tiesioginės problemos nelygybės - įtakos šios problemos tikslinės funkcijos vertei:
Δf(x) = b i y i
Išspręsdami ZLP naudojant simplekso metodą, kartu išsprendžiame ir dvigubą ZLP. Dvigubos problemos y i kintamųjų reikšmės optimaliame plane vadinamos objektyviai nustatytais arba dvigubais įverčiais. Taikomuose uždaviniuose dvigubi y i įverčiai dažnai vadinami paslėptomis, šešėlinėmis kainomis arba ribiniais išteklių įvertinimais.
Abipusių dvejopų problemų savybė
- Viename uždavinyje ieškoma tiesinės funkcijos maksimumo, kitoje – minimumo.
- Vienos problemos tiesinės funkcijos kintamųjų koeficientai yra laisvieji apribojimų sistemos nariai kitoje.
- Kiekvienas uždavinys pateiktas standartine forma, o maksimizavimo uždavinyje visos formos nelygybės ≤ , o minimizavimo uždavinyje visos formos nelygybės ≥ .
- Abiejų uždavinių apribojimų sistemų kintamųjų koeficientų matricos perkeliamos viena į kitą:
- Nelygybių skaičius vienos problemos apribojimų sistemoje sutampa su kitos problemos kintamųjų skaičiumi.
- Abiejose problemose yra kintamųjų neneigiamumo sąlygos.
Pusiausvyros teorema
2 problemaSukurkite dvigubą uždavinį į 1 uždavinį. Raskite jį sprendimas pagal pusiausvyros teoremą.
3x 1 +x 2 ≥12
x 1 +2x 2 ≥14
4x 1 +11x 2 ≥68
Pusiausvyros teorema
. Tegul X*=(x 1 *,...,x n *) ir Y*=(y 1 *,...,y n *) yra leistini planai dvejopų uždavinių porai simetriškai. Šie planai yra optimalūs, jei ir tik tenkinamos šios papildomos laisvumo sąlygos: 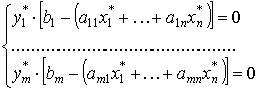

4 teorema leidžia nustatyti optimalų vienos iš dvejopų uždavinių poros sprendimą, sprendžiant kitą. Jei vienos problemos suvaržymas, pakeičiant optimalų sprendimą, virsta griežta nelygybe, tai atitinkamas dvigubas kintamasis optimaliame dvigubos problemos sprendime lygus 0. Jei optimaliame vienos problemos plane koks nors kintamasis yra teigiamas, tada jis yra lygus 0. tada atitinkamas dualinės problemos apribojimas yra lygtis.
Pateiksime ekonominį papildomo nelankstumo sąlygų aiškinimą. Jei optimaliame sprendime bet kurios žaliavos balas skiriasi nuo 0, tada ji bus visiškai sunaudota (resursų yra mažai). Jei žaliava nėra visiškai sunaudota (yra perteklius), tada jos įvertis yra 0. Taigi, mes nustatome, kad dvigubi įverčiai yra žaliavų trūkumo matas. Įvertis parodo, kiek padidės tikslo funkcijos reikšmė, kai atitinkamos žaliavos atsargos padidės 1 vienetu. Jei tam tikros rūšies gaminys yra įtrauktas į gamybos planą, tai jo gamybos kaštai sutampa su pagamintos prekės savikaina. Jei bet kokios rūšies gaminio gamybos kaštai yra didesni už prekės savikainą, tai produktas negaminamas.
Jei vienoje iš dvejopų uždavinių poros yra du kintamieji, ją galima išspręsti grafiškai, o tada dvigubos problemos sprendimą galima rasti naudojant 3 ir 4 teoremas. Tokiu atveju gali atsirasti 3 atvejai: abi problemos turi leistinus sprendimus, tik viena turi leistinų sprendimų problemą, abi problemos neturi įmanomų sprendimų.
2 pavyzdys
Sudarykite dvigubą uždavinį ir raskite jos sprendimą, naudodami pusiausvyros teoremą
x 2 -2x 3 +2x 4 -2x 5 ≤4
-2x 1 -2x 2 +2x 3 +2x 4 +x 5 ≥2
x i ≥0, i=1,5
Z=10x 1 -9x 2 -19x 3 -13x 4 -11x 5 → max, jei žinomas pradinės problemos sprendimas: Zmax=(3;4;0;0;0).
Sukurkime dvigubą problemą. Suderinkime nelygybių požymius su pradinės problemos tikslu. 
Z = 10x 1 -9x 2 -19x 3 -13x 4 -11x 5 → maks.
Dviguba problema: 
W=4 m. 1 -2 m. 2 → min
Raskime optimalų dvigubos problemos sprendimą, naudodami pusiausvyros teoremą. Užrašykime papildomo nelankstumo sąlygas.
y 1 (4-(x 2 -2x 3 +2x 4 -2x 5)) = 0
y 2 (-2-(2x 1 -2x 2 -2x 3 -2x 4 -x 5)) = 0
x 1 (-2y 2 -10) = 0
x 2 (y 1 -2y 2 +9) = 0
x 3 (-2y 1 -2y 2 +19) = 0
x 4 (2 m. 1 - 2 m. 2 +13) = 0
x 5 (-2y 1 -y 2 +11) = 0
Sukompiliuota sistema pakeisime optimalų pradinio uždavinio sprendimą: x 1 =3, x 2 =4, x 3 =0, x 4 =0, x 5 =0.
y 1 (4-(4-2 0+2 0-2 0)) = 0
y 2 (-2-(2 3-2 4-2 0-2 0-0)) = 0 W(y 1, y 2, y 3) = 12y 1 +31y 2 +18y 3 → maks. Pagal 3 teoremą Zmax=Wmin=100000.
Galiausiai Wmin=W(0; 4000/7; 32000/21) = 100000
Galimų judesių principo taikymas
Galimų poslinkių principas labai efektyvus tiriant plokštuminių mechanizmų pusiausvyrą, t.y. tie, kurių grandys juda plokštumose, lygiagrečiomis kokiai nors fiksuotai plokštumai. Supaprastintai galime daryti prielaidą, kad visi jo taškai ir nuorodos juda paties piešinio plokštuma.
Atsižvelgiant į tai, kad visos mechanizmo grandžių jungtys, taip pat ir išorinės jungtys yra idealios, jų reakcijas neįtraukiame. Tai lemia galimų poslinkių principo pranašumus, lyginant su geometrinės statikos (pusiausvyros lygčių) metodais.
Nepaisydami trinties, raskite ryšį tarp jėgų P Ir K, kuriame švaistiklio-slankiklio mechanizmas bus pusiausvyroje, jei jėga yra statmena O.A.(2.8 pav.).
Informuojant galimo judėjimo mechanizmą, o jėgų darbo sumą prilyginant nuliui P Ir K apie šį judėjimą gauname
P× dS B – Q×dS A = 0,
Kur dS A Ir dS B– galimų taškų judėjimo moduliai A Ir IN.
Judėjimas dS A statmenai O.A., dS B nukreiptas tiesia linija O.B. Norint nustatyti ryšį tarp dS B Ir dS A suraskime nuorodos MCS AB.Jis yra statmenų ir galimų taškų judėjimo krypčių sankirtoje A Ir IN. Šie judesiai yra tokie patys kaip ir taškų greitis A Ir IN, t.y.
Įvesdami kampo simbolius j Ir y, iš sinusų teoremos randame
Priklausomybė tarp galimų judesių dS A Ir dS B galima nustatyti naudojant taško greičio projekcijos teoremą A Ir B tiesiogiai AB. Naudodami šią teoremą galime parašyti:
dS A cos = dS B× jaukus,
Nagrinėjama problema galėtų būti išspręsta naudojant standžiosios kūno statikos metodus. Norėdami tai padaryti, turite sukurti kiekvienos mechanizmo grandies pusiausvyros lygtis (alkūnę OA, švaistiklis AB, slankiklis IN); šiuo atveju reikėtų atsižvelgti į nežinomas jungčių reakcijas (reakcijas vyriuose A Ir IN ir kreiptuvų, kuriais juda skaidrė, reakcija).
Sprendžiant tokio pobūdžio problemas, akivaizdus galimų poslinkių principo pranašumas; Šis metodas leidžia neįtraukti nežinomų ryšių reakcijos, nes šios reakcijos nėra įtrauktos į sistemos pusiausvyros sąlygą, išreikštą galimų poslinkių principu.
2.6. Galimų judesių principo taikymas
nustatyti ryšių reakcijas
Formuluojant galimų poslinkių principą reakcijos jėgos neatsiranda. Tačiau šioms jėgoms nustatyti galima efektyviai taikyti galimų poslinkių principą ir kuo sudėtingesnė konstrukcija, tuo didesni galimų poslinkių principo pranašumai, lyginant su geometrinėje statikoje naudojamais metodais (pusiausvyros lygčių braižymas ir sprendimas).
Statinės struktūros (struktūros) turi nulinį mobilumo laipsnį, t.y. yra subalansuoti dėl išorinių ir vidinių jungčių. Ant kūno uždėto standaus sandariklio formos jungtis riboja bet kokius jo judesius, todėl reakciją vaizduojame dviejų komponentų, nukreiptų išilgai koordinačių ašių, ir reaktyvaus momento. Šarnyrinė fiksuota atrama riboja kūno judėjimą dviem tarpusavyje statmenomis kryptimis, jo reakcija vaizduojama dviejų komponentų pavidalu išilgai koordinačių ašių.
Taikant išsivadavimo iš ryšių principą, galima atmesti vieną ryšį, kuris riboja kūno judėjimą viena kryptimi, pakeičiant jį reakcijos jėga.
Tais atvejais, kai jungtis neleidžia kūnui judėti keliomis kryptimis (fiksuota šarnyrinė atrama, standus įterpimas), ji pakeičiama kito tipo jungtimi, leidžiančia judėti reakcijos kryptimi, kurią norime nustatyti.
Norint nustatyti reaktyvųjį momentą standžiajame sandariklyje, jis pakeičiamas fiksuota vyrių atrama ir norimu reaktyviniu momentu (2.9 pav.).
Norint nustatyti standžiojo įdėjimo reakcijos horizontalųjį arba vertikalųjį komponentą, jis pakeičiamas strypo tipo jungtimi kreipikliuose ir norima reakcija (2.10, 2.11 pav.).
Tokiu būdu visų ryšių reakcijas galima nustatyti nuosekliai. Tokiu atveju kiekvieną kartą atmetamas ryšys, kurio reakciją reikia nustatyti, ir mechaninė sistema gauna vieną laisvės laipsnį.
Tais atvejais, kai jungtis neleidžia kėbului judėti keliomis kryptimis (fiksuota šarnyrinė atrama, standus įterpimas), jis nėra visiškai išmetamas, o tik pakeičiamas paprastesniu. Kaip tai daroma, parodyta fig. 2.12.
Nustatydami jo reakcijas parodysime šarnyrinės fiksuotos atramos pakeitimo galimybes.
Pažvelkime į komponentų palaikymo reakcijų nustatymo pavyzdžius
dizaino.
Antagoniškame žaidime natūralu, kad optimaliu rezultatu galima laikyti tokį rezultatą, kuriame bet kuriam žaidėjui nenaudinga nuo jo nukrypti. Toks rezultatas (x*,y*) vadinamas pusiausvyros situacija, o optimalumo principas, pagrįstas pusiausvyros situacijos radimu, vadinamas pusiausvyros principu.
Apibrėžimas. Matricos žaidime su matmenų matrica rezultatas yra toks pusiausvyros situacija arba balno taškas, jei
Balno taške matricos elementas yra ir minimumas savo eilutėje, ir maksimumas stulpelyje. Žaidime iš 2 pavyzdžio elemento a 33 yra balno taškas. Optimalios strategijos šiame žaidime yra trečios abiem žaidėjams. Jei pirmasis žaidėjas nukrypsta nuo trečiosios strategijos, jis pradeda laimėti mažiau nei a 33. Jei antrasis žaidėjas nukrypsta nuo trečiosios strategijos, jis pradeda prarasti daugiau nei a 33. Taigi abiem žaidėjams nėra nieko geriau, kaip nuosekliai siekti trečiosios strategijos.
Optimalaus elgesio principas: jei matricos žaidime yra balno taškas, tai optimalus pasirinkimas yra tašką atitinkanti strategija. Kas atsitiks, jei žaidime yra daugiau nei vienas balno taškas?
Teorema. Leisti ![]() du savavališki balno taškai matricos žaidime. Tada:
du savavališki balno taškai matricos žaidime. Tada:
Įrodymas. Iš pusiausvyros situacijos apibrėžimo turime:
Pakeiskime , į kairę nelygybės pusę (2.8), o į dešinę pusę, į kairę nelygybės pusę (2.9) ir į dešinę pusę, . Tada gauname:
Tai reiškia lygybę:
Iš teoremos išplaukia, kad išmokėjimo funkcija visose pusiausvyros situacijose įgyja tą pačią reikšmę. Dėl to ir vadinamas numeris žaidimo kaina. Ir yra vadinamos strategijos, atitinkančios bet kurį balno tašką optimalios strategijos atitinkamai 1 ir 2 žaidėjai. Remiantis (2.7), visos optimalios žaidėjo strategijos yra keičiamos.
Optimalus žaidėjų elgesys nepasikeis, jei žaidimo strategijų rinkinys išliks toks pat, o išmokėjimo funkcija padauginama iš teigiamos konstantos (arba prie jos pridedamas pastovus skaičius).
Teorema. Kad matricos žaidime egzistuotų balno taškas (i*,j*), būtina ir pakanka, kad maksimumas būtų lygus minimax:
(2.10) ![]()
Įrodymas. Būtinybė. Jei (i*,j*) yra balno taškas, tada pagal (2.6):
(2.11) ![]()
Tuo pačiu metu turime:
(2.12) ![]()
Iš (2.11) ir (2.12) gauname:
(2.13) ![]()
Panašiai samprotaudami, gauname lygybes:
Taigi,
![]()
Kita vertus, atvirkštinė nelygybė (2.5) galioja visada, todėl (2.10) galioja.
Tinkamumas. Tegul (2.10) yra tiesa. Įrodykime balno taško egzistavimą. Mes turime:
Pagal lygybę (2.10) nelygybės (2.15) ir (2.16) virsta lygybėmis. Tada mes turime:
![]()
![]()
Teorema įrodyta. Kelyje tai buvo įrodyta bendrą reikšmę maximin ir minimax yra lygūs žaidimo kainai.
Mišrus žaidimo išplėtimas
Apsvarstykite matricinį žaidimą G. Jei jame yra pusiausvyros situacija, tai minimax yra lygi maximin. Be to, kiekvienas žaidėjas gali suteikti kitam žaidėjui informaciją apie savo optimalią strategiją. Jo priešininkas iš šios informacijos neturės jokios papildomos naudos. Dabar tarkime, kad žaidime G nėra pusiausvyros situacijos. Tada:
Šiuo atveju minimalios ir maksimalios strategijos nėra stabilios. Žaidėjai gali turėti paskatų nukrypti nuo savo atsargių strategijų dėl galimybės laimėti daugiau laimėjimų, bet ir su rizika pralaimėti, tai yra gauti mažesnį laimėjimą nei naudojant atsargią strategiją. Naudojant rizikingas strategijas, informacijos apie jas perdavimas priešininkui turi žalingų pasekmių: žaidėjas automatiškai gauna mažesnį atlygį nei naudojant atsargią strategiją.
3 pavyzdys. Tegul žaidimo matrica turi tokią formą:
Tokiai matricai, t.y. nėra pusiausvyros situacijos. Atsargios žaidėjų strategijos yra i*=1, j*=2. Tegul 2 žaidėjas laikosi strategijos j*=2, o 1 žaidėjas pasirenka strategiją i=2. tada pastarasis gaus išmoką 3, tai yra dviem vienetais daugiau nei maksimalus. Tačiau jei 2 žaidėjas atspėja apie 1 žaidėjo planus, jis pakeis savo strategiją į j=1, o tada pirmasis gaus 0 išmoką, ty mažesnę nei jo maksimumas. Panašus samprotavimas gali būti atliktas ir antrajam žaidėjui. Apskritai galime daryti išvadą, kad nuotykių strategijos naudojimas gali duoti didesnį rezultatą nei garantuota atskirame žaidime, tačiau jos naudojimas yra susijęs su rizika. Kyla klausimas, ar įmanoma patikimą atsargią strategiją derinti su nuotykių kupinančia taip, kad padidėtų jūsų vidutinis laimėjimas? Iš esmės kyla klausimas, kaip paskirstyti laimėjimus žaidėjams (2,17)?
Pasirodo, protingas sprendimas yra naudoti mišrią strategiją, tai yra atsitiktinis grynų strategijų pasirinkimas. Prisiminkime tai 1 žaidėjo strategija vadinama mišria, jei jis pasirinks i-tą eilutę su tam tikra tikimybe p i .Šią strategiją galima identifikuoti su tikimybių skirstiniu ![]() daugelyje eilučių. Tarkime, kad pirmasis žaidėjas turi m grynų strategijų, o antrasis žaidėjas turi n grynų strategijų. Tada jų mišrios strategijos yra tikimybiniai vektoriai:
daugelyje eilučių. Tarkime, kad pirmasis žaidėjas turi m grynų strategijų, o antrasis žaidėjas turi n grynų strategijų. Tada jų mišrios strategijos yra tikimybiniai vektoriai:
(2.18) 
Apsvarstykite dvi galimas mišrias strategijas pirmajam žaidėjui iš 3 pavyzdžio:  . Šios strategijos skiriasi tikimybių pasiskirstymu tarp grynųjų strategijų. Jei pirmuoju atveju matricos eilutes žaidėjas pasirenka vienodomis tikimybėmis, tai antruoju atveju – skirtingomis. Kai kalbame apie mišrią strategiją, turime omenyje atsitiktinis pasirinkimas ne pasirinkimas „atsitiktinai“, o pasirinkimas, pagrįstas atsitiktinio mechanizmo, suteikiančio mums reikalingą tikimybių skirstinį, veikimu. Taigi monetos metimas puikiai tinka įgyvendinti pirmą iš mišrių strategijų. Žaidėjas pasirenka pirmąją arba antrąją eilutę, priklausomai nuo to, kaip nukrenta moneta. Vidutiniškai žaidėjas pirmąją ir antrąją eilutę rinksis vienodai dažnai, tačiau pasirinkimui tam tikroje žaidimo iteracijoje netaikoma jokia fiksuota taisyklė ir jis turi maksimalų slaptumo laipsnį: iki atsitiktinio mechanizmo įgyvendinimo, tai nežinoma net pačiam pirmam žaidėjui. Burtų traukimo mechanizmas puikiai tinka įgyvendinti antrąją mišrią strategiją. Žaidėjas paima septynis vienodus popieriaus lapus, tris iš jų pažymėdamas kryželiu ir įmeta į kepurę. Tada atsitiktinai jis ištraukia vieną iš jų. Pagal klasikinę tikimybių teoriją jis ištrauks popieriaus lapą su kryželiu tikimybe 3/7, o tuščią popieriaus lapą – 4/7. Toks braižybos mechanizmas gali įgyvendinti bet kokias racionalias tikimybes.
. Šios strategijos skiriasi tikimybių pasiskirstymu tarp grynųjų strategijų. Jei pirmuoju atveju matricos eilutes žaidėjas pasirenka vienodomis tikimybėmis, tai antruoju atveju – skirtingomis. Kai kalbame apie mišrią strategiją, turime omenyje atsitiktinis pasirinkimas ne pasirinkimas „atsitiktinai“, o pasirinkimas, pagrįstas atsitiktinio mechanizmo, suteikiančio mums reikalingą tikimybių skirstinį, veikimu. Taigi monetos metimas puikiai tinka įgyvendinti pirmą iš mišrių strategijų. Žaidėjas pasirenka pirmąją arba antrąją eilutę, priklausomai nuo to, kaip nukrenta moneta. Vidutiniškai žaidėjas pirmąją ir antrąją eilutę rinksis vienodai dažnai, tačiau pasirinkimui tam tikroje žaidimo iteracijoje netaikoma jokia fiksuota taisyklė ir jis turi maksimalų slaptumo laipsnį: iki atsitiktinio mechanizmo įgyvendinimo, tai nežinoma net pačiam pirmam žaidėjui. Burtų traukimo mechanizmas puikiai tinka įgyvendinti antrąją mišrią strategiją. Žaidėjas paima septynis vienodus popieriaus lapus, tris iš jų pažymėdamas kryželiu ir įmeta į kepurę. Tada atsitiktinai jis ištraukia vieną iš jų. Pagal klasikinę tikimybių teoriją jis ištrauks popieriaus lapą su kryželiu tikimybe 3/7, o tuščią popieriaus lapą – 4/7. Toks braižybos mechanizmas gali įgyvendinti bet kokias racionalias tikimybes.
Tegul žaidėjai laikosi mišrių strategijų (2.18). Tada pirmojo žaidėjo atlyginimas tam tikroje žaidimo iteracijoje yra atsitiktinis kintamasis: v(X,Y). Kadangi žaidėjai renkasi strategijas nepriklausomai vienas nuo kito, tai pagal tikimybių daugybos teoremą tikimybė pasirinkti rezultatą (i, j) su laimėjimu yra lygi tikimybių sandaugai. Tada atsitiktinio dydžio pasiskirstymo dėsnis v(X,Y) pateiktą toliau pateiktoje lentelėje

Dabar leiskite žaidimui tęstis neribotą laiką. Tada vidutinis laimėjimas tokiame žaidime yra lygus matematiniam vertės lūkesčiui v(X,Y).
(2.19) ![]()
Esant ribotam, bet pakankamai dideliam žaidimo iteracijų skaičiui, vidutinė išmoka šiek tiek skirsis nuo vertės (2,19).
Pavyzdys 4. Apskaičiuokite vidutinį žaidimo laimėjimą (2,19) pagal 3 pavyzdį, kai žaidėjai naudoja šias strategijas:  . Išmokėjimo matrica ir tikimybių matrica atrodo taip:
. Išmokėjimo matrica ir tikimybių matrica atrodo taip:

Raskime vidurkį:
Taigi vidutinė išmoka (2,20) yra tarpinė tarp maximin ir minimax.
Kadangi bet kuriai mišrių strategijų X ir Y porai galima apskaičiuoti vidutinę žaidimo vertę, kyla problemų ieškant optimalios strategijos. Natūralu pradėti tyrinėjant atsargias strategijas. Pirmojo žaidėjo atsargi strategija suteikia jam maksimalų. Kruopšti antrojo žaidėjo strategija neleidžia pirmajam laimėti daugiau nei minimax. Reikšmingiausias rezultatas priešingų interesų žaidimų teorijoje yra toks:
Teorema. Kiekvienas matricos žaidimas turi pusiausvyros situaciją mišriose strategijose. Įrodyti šią teoremą nėra lengva. Šiame kurse jis praleistas.
Pasekmės: Pusiausvyros situacijos egzistavimas reiškia, kad maximin yra lygus minimax, todėl bet koks matricos žaidimas turi kainą. Optimali strategija pirmajam žaidėjui yra maksimali strategija. Optimali strategija antrajam yra minimax. Kadangi optimalių strategijų paieškos problema buvo išspręsta, mes sakome, kad bet koks matricos žaidimas išsprendžiamas dėl įvairių mišrių strategijų.
2x2 žaidimo sprendimas
Pavyzdys 5. Išspręskite žaidimą. Nesunku patikrinti, ar nėra balno taško. Pažymime optimalią pirmojo žaidėjo strategiją (x, 1-x) yra stulpelio vektorius, bet patogumo dėlei jį rašome kaip eilutę. Pažymime optimalią antrojo žaidėjo strategiją (y, 1-y).
Pirmojo žaidėjo atlyginimas yra atsitiktinis dydis, kurio pasiskirstymas yra toks:
| v(x,y) | 2 | -1 | -4 | 7 |
| p | xy | x(1-y) | (1–x) m | (1–x) (1–y) |
Mes randame vidutinį pirmojo žaidėjo pasipelnymą – atsitiktinio dydžio matematinį lūkestį v(x,y):
Paverskime šią išraišką:

Šis matematinis lūkestis susideda iš pastovios (5/7) ir kintamos dalies: 14 (x-11/14) (y-8/14). Jei vertė y skiriasi nuo 8/14, tada pirmasis žaidėjas visada gali pasirinkti X tokiu būdu, kad kintamoji dalis būtų teigiama, padidinant jūsų laimėjimą. Jei vertė X skiriasi nuo 11/14, tada antrasis žaidėjas visada gali pasirinkti y tokiu būdu, kad kintamoji dalis būtų neigiama, sumažinant pirmojo žaidėjo laimėjimą. Taigi balno taškas nustatomas pagal lygybes: x*=11/14, y*=8/14.
2.5 Žaidimo sprendimas
Mes parodysime, kaip išspręsti tokius žaidimus naudodami pavyzdį.
Pavyzdys 6. Išspręskite žaidimą  . Pasirūpiname, kad nebūtų balno taško. Pažymime mišrią pirmojo žaidėjo strategiją X=(x, 1-x) yra stulpelio vektorius, bet patogumo dėlei jį rašome kaip eilutę.
. Pasirūpiname, kad nebūtų balno taško. Pažymime mišrią pirmojo žaidėjo strategiją X=(x, 1-x) yra stulpelio vektorius, bet patogumo dėlei jį rašome kaip eilutę.
Tegul pirmasis žaidėjas naudoja X strategiją, o antrasis žaidėjas naudoja savo j-tas švarus strategija. Pažymime vidutinį pirmojo žaidėjo atlyginimą šioje situacijoje kaip . Mes turime:
Atkarpoje pavaizduokime funkcijų (2.21) grafikus.

Taško, esančio bet kurioje tiesioje atkarpoje, ordinatės atitinka pirmojo žaidėjo laimėjimą situacijoje, kai jis naudoja mišrią strategiją (x, (1-x)), o antrasis žaidėjas – atitinkama grynoji strategija. Pirmojo žaidėjo garantuotas rezultatas yra apatinis tiesių linijų šeimos vokas (sulaužytas ABC). Aukščiausias šios nutrūkusios linijos taškas (taškas B) yra maksimalus garantuotas žaidėjo 1 rezultatas. Taško B abscisė atitinka optimalią pirmojo žaidėjo strategiją.
Kadangi norimas taškas B yra linijų ir sankirta, jo abscisę galima rasti kaip lygties sprendimą:
Taigi optimali pirmojo žaidėjo mišri strategija yra (5/9, 4/9). Taško B ordinatė yra žaidimo kaina. Jis lygus:
(2.22) 
Atkreipkite dėmesį, kad linija, atitinkanti antrojo žaidėjo antrąją strategiją, eina virš taško B. Tai reiškia, kad jei pirmasis žaidėjas naudoja savo optimalią strategiją, o 2 žaidėjas naudoja antrąją, tada antrojo žaidėjo praradimas padidėja, palyginti su strategijų naudojimu. 1 arba 3. Taigi antroji strategija neturėtų dalyvauti optimalioje antrojo žaidėjo strategijoje. 2 žaidėjo optimali strategija turėtų atrodyti taip: ![]() . Grynos antrojo žaidėjo 1 ir 3 strategijos, kurios optimalioje strategijoje turi ne nulį komponentų, paprastai vadinamos reikšmingas. 2 strategija vadinama nereikšmingas. Iš aukščiau pateikto paveikslo, taip pat iš lygybės (2.22) matyti, kad kai pirmasis žaidėjas naudoja savo optimalią strategiją, antrojo žaidėjo atsipirkimas nepriklauso nuo to, kurią iš jo esminių strategijų jis naudoja. Jis taip pat gali taikyti bet kokią mišrią strategiją, susidedančią iš reikšmingų (ypač optimalią), o laimėjimai šiuo atveju nepasikeis. Visiškai panašus teiginys galioja ir priešingu atveju. Jei antrasis žaidėjas naudoja savo optimalią strategiją, tai pirmojo žaidėjo laimėjimas nepriklauso nuo to, kurią iš jo esminių strategijų jis naudoja ir yra lygus žaidimo kainai. Naudodamiesi šiuo teiginiu, randame optimalią antrojo žaidėjo strategiją.
. Grynos antrojo žaidėjo 1 ir 3 strategijos, kurios optimalioje strategijoje turi ne nulį komponentų, paprastai vadinamos reikšmingas. 2 strategija vadinama nereikšmingas. Iš aukščiau pateikto paveikslo, taip pat iš lygybės (2.22) matyti, kad kai pirmasis žaidėjas naudoja savo optimalią strategiją, antrojo žaidėjo atsipirkimas nepriklauso nuo to, kurią iš jo esminių strategijų jis naudoja. Jis taip pat gali taikyti bet kokią mišrią strategiją, susidedančią iš reikšmingų (ypač optimalią), o laimėjimai šiuo atveju nepasikeis. Visiškai panašus teiginys galioja ir priešingu atveju. Jei antrasis žaidėjas naudoja savo optimalią strategiją, tai pirmojo žaidėjo laimėjimas nepriklauso nuo to, kurią iš jo esminių strategijų jis naudoja ir yra lygus žaidimo kainai. Naudodamiesi šiuo teiginiu, randame optimalią antrojo žaidėjo strategiją.




