Přímka definovaná průsečíkem dvou rovin. Obecné rovnice přímky jako průsečíku dvou rovin Najděte rovnici průsečíku přímky dvou rovin online

Každou přímkou v prostoru prochází nespočet rovin. Jakékoli dva z nich, které se protínají, jej definují v prostoru. V důsledku toho rovnice jakýchkoli dvou takových rovin, uvažované společně, představují rovnice této přímky.

Obecně jakékoli dvě nerovnoběžné roviny dané obecnými rovnicemi

určit přímku jejich průsečíku. Tyto rovnice se nazývají obecné rovnice rovný

Vstupenka 6 Zapište výraz pro úhel mezi přímkou a rovinou, podmínku rovnoběžnosti a kolmosti přímky a roviny.

Úhel mezi přímkou a rovinou budeme nazývat úhel, který svírá přímka a její průmět do roviny. Nechť jsou přímky roviny dány rovnicemi

Uvažujme vektory a . Pokud je úhel mezi nimi ostrý, pak to bude , kde φ je úhel mezi přímkou a rovinou. Pak .

Pokud je úhel mezi vektory a tupý, pak se rovná . Proto . Proto v každém případě. Když si vzpomeneme na vzorec pro výpočet kosinusu úhlu mezi vektory, dostaneme .

Podmínka kolmosti přímky a roviny. Přímka a rovina jsou kolmé právě tehdy, když směrový vektor přímky a normálový vektor roviny jsou kolineární, tzn. .

Podmínka rovnoběžnosti mezi přímkou a rovinou. Přímka a rovina jsou rovnoběžné právě tehdy, když jsou vektory a kolmé.

Vstupenka 7. Definujte elipsu. Napište rovnici elipsy v kanonickém tvaru. Vrcholy, ohniska, osy a excentricita elipsy.

Definice: Elipsa je geometrické místo bodů v rovině, pro každý z nich je součet vzdáleností ke dvěma daným bodům téže roviny, nazývaným ohniska elipsy, konstantní hodnotou.

Nechat F 1 a F 2 – ohniska elipsy. Start Ó souřadnicové systémy budou umístěny uprostřed segmentu F 1 F 2. Osa Vůl nasměrujme osu podél tohoto segmentu Oj– kolmo k tomuto segmentu (obr.).

Definice: Nazývají se průsečíky elipsy s jejími osami symetrie vrcholová elipsa a, střed symetrie – střed elipsy, segment mezi dvěma vrcholy obsahující ohniska se nazývá hlavní osa elipsy, polovina jeho délky – hlavní poloosa elipsy. Úsek mezi vrcholy na ose symetrie, který neobsahuje ohniska, se nazývá vedlejší osa elipsy, polovina jeho délky je vedlejší osa. Množství se nazývá excentricita elipsy.

Pokud je elipsa dána kanonickými rovnicemi, pak její vrcholy mají souřadnice (– A;0), (A;0),(0; –b), (0;b), hlavní poloosa je A, vedlejší vedlejší osa je rovna b. Velikost C, což je polovina vzdálenosti mezi ohnisky, se určí ze vzorce C 2 = A 2 – b 2 .

Excentricita elipsy charakterizuje stupeň protažení elipsy. Čím blíže je excentricita nule, tím více se elipsa podobá kruhu. Čím blíže je excentricita 1, tím je elipsa protáhlejší. Všimněte si, že podle definice pro elipsu 0< <1.

Rovnice se nazývá rovnice kanonické elipsy.

Vstupenka 8 Definujte hyperbolu. Napište rovnici hyperboly v kanonickém tvaru. Vrcholy, ohniska, osy, asymptoty a excentricity hyperboly,

Definice: Hyperbola je těžiště bodů v rovině, pro každý z nich je absolutní hodnota rozdílu vzdáleností ke dvěma pevným bodům téže roviny, nazývaná ohniska hyperboly, konstantní hodnotou.

Stejně jako v případě elipsy si pro získání rovnice hyperboly zvolíme vhodný souřadnicový systém. Počátek souřadnic se nachází uprostřed segmentu mezi ohnisky, osou Vůl Nasměrujme jej podél tohoto segmentu a ordináta je na něj kolmá.

Rovnice se nazývá kanonická rovnice nadsázka.

Hyperbola má dvě vzájemně kolmé osy symetrie, z nichž jedna obsahuje ohniska hyperboly a střed symetrie. Pokud je hyperbola dána kanonickou rovnicí, pak její osy symetrie jsou souřadnicové osy Vůl A Oj a počátek je středem symetrie hyperboly.

Definice: Průsečíky hyperboly definované kanonickou rovnicí s osou Vůl jsou nazývány vrcholy hyperboly, segment mezi nimi se nazývá reálná osa hyperboly. Úsek pořadnicové osy mezi body (0;– b) a (0; b) se nazývá pomyslná osa. Čísla A A b se nazývají skutečné a imaginární poloosy hyperboly, resp. Počátek souřadnic se nazývá její střed. Množství se nazývá excentricita nadsázka.

Komentář: Od rovnosti b 2 = C 2 – A 2 z toho vyplývá C>A, to znamená, že hyperbola má >1. Excentricita charakterizuje úhel mezi asymptotami, čím blíže k 1, tím menší je tento úhel.

Vstupenka 9. Definujte parabolu. Napište rovnici paraboly v kanonickém tvaru. Paní ředitelko, ohnisko paraboly

Parabola je těžiště bodů v rovině, které jsou stejně vzdálené od daného bodu F a dané přímky d, která daným bodem neprochází. Tato geometrická definice vyjadřuje režijní vlastnost paraboly.

Směrová vlastnost paraboly Bod F se nazývá ohnisko paraboly, přímka d je přímka paraboly, střed O kolmice spadající z ohniska k přímce je vrchol paraboly, vzdálenost p od ohnisko na přímku je parametr paraboly a vzdálenost p2 od vrcholu paraboly k jejímu ohnisku je ohnisková vzdálenost (obr.a). Přímka kolmá na směrovou přímku a procházející ohniskem se nazývá osa paraboly (ohnisková osa paraboly). Úsek FM spojující libovolný bod M paraboly s jeho ohniskem se nazývá ohniskový poloměr bodu M. Úsek spojující dva body paraboly se nazývá tětiva paraboly.

Pro libovolný bod paraboly je poměr vzdálenosti k ohnisku ke vzdálenosti k přímce roven jedné. Porovnáním režijních vlastností elipsy, hyperboly a paraboly docházíme k závěru, že excentricita paraboly podle definice rovné jedné

.Geometrická definice paraboly , vyjadřující jeho režijní vlastnost, je ekvivalentní jeho analytické definici - přímce definované kanonickou rovnicí paraboly:

Vstupenka 10. Co je čtvercová, jednotková, symetrická, ortogonální matice. Definujte transponovanou a inverzní matici.

Definice 1.Matice je obdélníková tabulka čísel obsahující - řádky a - sloupce. .

Definice 2.Čísla, kterým se říká Maticové příkazy(nebo se říká, že matice má velikost)

Definice 3.Čísla obsažená v této matici se nazývají její Prvky.

1. Definice 4. Matice se nazývá Náměstí pokud je počet řádků roven počtu sloupců. V případě čtvercové matice se zavádějí pojmy Hlavní úhlopříčka(to jsou čísla - ) a Boční úhlopříčka(to jsou čísla -).

2.Symetrický(Symetrická) je čtvercová matice, jejíž prvky jsou symetrické kolem hlavní diagonály. Formálněji se matice nazývá symetrická, takže .

To znamená, že se rovná své transponované matici:

3. Jednotková matice se nazývá diagonální matice, ve které jsou všechny diagonální prvky rovny jedné. Například matice identity třetího řádu je matice

Ortogonální matice

Čtvercová matice A, pro který A-1 = AT volal ortogonální matice. Základní vlastnosti ortogonální matice: Modul determinantu ortogonální matice je roven jedné. Tato vlastnost vyplývá z vlastností determinantů:

Součet čtverců prvků libovolného sloupce ortogonální matice se rovná jedné.

Bodový součin řádku se sebou samým je 1 as jakýmkoli jiným řádkem je 0. Totéž platí pro sloupce.

Součet součinů prvků libovolného řádku ortogonální matice odpovídajícími prvky jiného řádku je nulový.

Inverzní matice je matice, která po vynásobení zprava i zleva danou maticí dává matici identity Označme inverzní matici A přes , pak podle definice dostaneme: Kde E– matice identity.

Inverzní matice neexistuje pro všechny matice. Nezbytnou a postačující podmínkou pro nedegeneraci je

det( A) ≠ 0 nebo pořadí ( A) = N.

Vlastnosti inverzních matic

· , kde označuje determinant.

· pro libovolné dvě invertibilní matice a .

· , kde označuje transponovanou matici.

· pro libovolný koeficient.

· Pokud je nutné řešit soustavu lineárních rovnic , (b je nenulový vektor) kde je požadovaný vektor, a pokud existuje, pak . V opačném případě je buď rozměr prostoru řešení větší než nula, nebo neexistují žádná řešení.

Transponovaná matice- matice získaná z původní matice nahrazením řádků sloupci.

Formálně je transponovaná matice pro matici velikosti matice velikosti definovaná jako .

Vstupenka 11. Co jsou ekvivalentní matice? Vyjmenujte elementární transformace matic. Co můžeme říci o řadách ekvivalentních matic?

Definice. Matice získané jako výsledek elementární transformace se nazývají ekvivalent.

Elementární transformace nad řadami matic Následující převody řetězců se nazývají:

1. násobení řetězce nenulovým číslem;

2. přeskupení dvou linek;

3. přidání dalšího řádku matice k jednomu řádku matice vynásobeného nějakým nenulovým číslem.

4. Pokud se přechází z matice do matice pomocí ekvivalentních transformací přes řádky, pak se takové matice nazývají ekvivalent a označují .

5. Elementární transformační metoda

6. Hodnost matice se rovná počtu nenulových řádků v matici po jejím zmenšení na echelonový tvar pomocí elementárních transformací přes řádky matice.

Vstupenka 12, Co je základní moll. Vyslovte základní vedlejší větu.

Definice. Hodnost matice A je maximální řád nenulové minority (minor je determinant čtvercové matice). Označeno .

Definice. Menší, která určuje hodnost matice, se nazývá Basis minor. Řádky a sloupce, které tvoří BM, se nazývají základní řádky a sloupce.

Definice. Sloupový systém se nazývají lineárně závislá čísla, která nejsou všechna rovna nule a taková, že:

Základní vedlejší věta

Sloupce matice zahrnuté v základu minor tvoří lineárně nezávislý systém. Jakýkoli sloupec matice je lineárně vyjádřen prostřednictvím zbývajících sloupců základní minority.

V matici velikostí se minoritní řád t. řádu nazývá základem, pokud je nenulový a všechny vedlejší řády -ro jsou nulové nebo vůbec neexistují.

Následek. Pokud jsou všechny sloupce matice lineárně vyjádřeny pomocí sloupců, které tvoří lineárně nezávislý systém, pak je hodnost matice .

Vstupenka 13 Co je homogenní a nehomogenní soustava rovnic. To, čemu se říká řešení soustavy rovnic. Vysvětlete pojmy: kompatibilní soustava rovnic, nekonzistentní soustava rovnic. Které soustavy rovnic se nazývají ekvivalentní?

Definice 1. Pokud jsou všechny volné členy rovny nule, pak se systém nazývá homogenní a jinak nehomogenní.

Definice 2.Řešením systému je sada nčísla S 1 , S 2 , …, S n , které, když se do systému dosadí místo neznámých, bude mít za následek mčíselné identity.

Definice 3. Systém se nazývá kompatibilní (nekompatibilní), pokud má alespoň jedno řešení (nemá žádná řešení).

Definice 4. Konzistentní systém lineárních algebraických rovnic se nazývá určitý (neurčitý), pokud má jedinečné řešení (množinu řešení).

Definice.

Jsou nazývány dva systémy lineárních rovnic ekvivalent (ekvivalent), pokud mají stejná řešení.

Ekvivalentní soustavy získáme zejména elementárními transformacemi soustavy za předpokladu, že se transformace provádějí pouze na řádcích soustavy.

Vstupenka 14 Co je základní soustava řešení homogenní soustavy rovnic. To, čemu se říká obecné řešení homogenní soustavy rovnic.

Definice. Základem prostoru řešení soustavy lineárních homogenních rovnic se nazývá její základní systém řešení.

Věta o struktuře obecného řešení homogenní soustavy rovnic:

Jakékoli řešení homogenní soustavy lineárních rovnic je určeno vzorcem

Kde X 1 , X 2 , … , Xn − r- základní soustava řešení homogenní soustavy lineárních rovnic a C 1 , C 2 , … , Cn − r- libovolné konstanty.

Vlastnosti obecného řešení homogenní soustavy rovnic:

1. Pro libovolné hodnoty C 1 , C 2 , … , Cn − r X, definovaný vzorcem (3), je řešením systému (1).

2. Bez ohledu na rozhodnutí X 0, jsou tam čísla C 1 0 , … , Cn − r 0 takové, že

Závěr: Chcete-li najít základní systém a obecné řešení homogenního systému, musíte najít základ jádra odpovídajícího lineárního operátoru.

Vstupenka 16. Definujte lineární prostor a formulujte jeho vlastnosti.

hromada L volal lineární nebo vektorový prostor , pokud jsou pro všechny prvky (vektory) této množiny definovány operace sčítání a násobení číslem a platí následující:

1. Každá dvojice prvků X A y z L reaguje prvek X + y z L , volal množstvíX A y, a:

X + y = y+x− sčítání je komutativní;

X + (y + z) = (x + y) + z− sčítání je asociativní;

X +0 = X− je jen jeden nulaživel 0 (X +0 = X pro každého X z L );

X + (− X)= 0 − pro každý prvek X z L je jen jeden naprotiživel −x (x + (−x) = 0 pro každého X z L) .

2. Každý pár X a α, kde α − číslo a X prvek z L , odpovídá prvku α X, volal práceα AX, a:

α·(β · X) = (α·β) · X− násobení číslem je asociativní: ;

1· X = X− pro jakýkoli prvek X z L .

3. Operace sčítání a násobení číslem souvisí s následujícími vztahy:

α·( X + y) = α· X + α· y− násobení číslem je distributivní vzhledem k sčítání prvků;

(α + β )· X = α· X + β · X− násobení vektorem je distributivní vzhledem k sčítání čísel.

Vstupenka 17. Podprostor lineárního prostoru. Jeho vlastnosti. Lineární skořepina.

Definice lineárního podprostoru

Neprázdná podmnožina L lineárního prostoru V se nazývá lineární podprostor prostor V pokud

1) u+v∈L ∀u,v∈L (podprostor je uzavřen vzhledem k operaci sčítání);

2) λv∈L ∀v∈L a libovolné číslo λ (podprostor je uzavřen vzhledem k operaci násobení vektoru číslem).

Nemovitost 1 Každý podprostor lineárního prostoru R je lineární prostor.

Nemovitost 2 dim M ≤ dim Rn.

Vlastnost 3 (o dokončení základu). Jestliže (ep)k je báze v podprostoru M lineárního prostoru Rn ak< n, то можно так выбрать элементы в Rn ek+1, ek+2, . . . , en, что (ep)n будет базисом в Rn.

Definice: Lineární skořepina je množina vektorů, které definují lineární podprostor. Přísně vzato, lineární obal je množina všech lineárních kombinací daných vektorů. Uvedeme také vlastnosti:

Vstupenka 18. Definujte euklidovský prostor. Vysvětlete fungování vektorové normalizace.

Definice Nechť V je vektorový prostor. O skalárním součinu se říká, že je dán ve V, pokud jsou libovolné dva vektory x, y ∈ V spojeny s reálným číslem, které se nazývá skalární součin těchto vektorů a značí xy nebo (x, y), takže platí následující podmínky: splněny (zde x, y, z jsou libovolné vektory z V a

t - libovolné reálné číslo):

1) xy = yx (skalární součin je komutativní);

2) (tx)y = t(xy);

3) (x + y)z = xz + yz (skalární součin je distributivní s ohledem na sčítání);

4) xx >=0 a xx = 0 právě tehdy, když x = 0.

Vektorový prostor, ve kterém je skalární součin specifikován, se nazývá euklidovský. Vlastnosti 1)–4) se nazývají axiomy euklidovského prostoru.

Vektor se nazývá normalizované nebo individuální, je-li jeho délka rovna jedné. Normalizovat libovolný nenulový vektor znamená vydělit ho jeho délkou. Výsledkem je jednotkový vektor kosměrný k původnímu.
Skalární součin libovolného vektoru a jednotkového vektoru dá přesnou délku průmětu tohoto vektoru do směru jednotkového vektoru. Abychom získali nejen délku, ale i samotnou vektorovou projekci, musíme tuto délku vynásobit naším jednotkovým vektorem:

Vstupenka 19 Co je ortonormální základ? Vysvětlete Gram-Schmidtův ortogonalizační proces na příkladu dvourozměrné báze.

Ortonormální systém sestávající z n vektory n-rozměrný euklidovský prostor, tvoří základ tohoto prostoru. Takový základ se nazývá ortonormální základ.

Li E 1 , E 2 , ..., en -ortonormální základ n-rozměrný euklidovský prostor a

X = X 1 e 1 + X 2 e 2 + ... + X n E n - vektorový rozklad X podle tohoto základu pak souřadnice Xi vektor X na ortonormálním základě se vypočítají pomocí vzorců Xi =(x, napři ), i= 1, 2, ..., n.

GRAMA-SCHMIDT, Je dán lineárně nezávislý systém vektorů b 1 , b 2 , …, b l , a l+1 , …, a n l ≥ 1(1)bude označena část, ke které je ortogonální b l+1 ortogonální složka vektoru a l+1 vzhledem k ortogonálnímu systému b 1, b 2, …, b l. Potom 1. Vektorový systém b 1 , b 2 , …, b l , b l+1 , a l+2 , …, a n(2) je ekvivalentní (1).

2. Systém vektorů (2) je lineárně nezávislý a je jeho součástí b 1, b 2, …, b l, b l+1– ortogonální.Pojmem ortogonální složky popíšeme proces transformace lineárně nezávislého systému a 1, a 2, …, a n do ortogonálního systému b 1, b 2, …, b n nenulové vektory, což je tzv ortogonalizace systému a 1, a 2, …, a n.Tento proces se skládá z n-kroků, n-počet vektorů v původním systému a 1, a 2, …, a n.

1 krok. Věříme b 1 = a 1 a dostaneme systém b 1, a 2, …, a n

Krok 2. Nahradíme vektor v systému (3) a 2 ortogonální složka vzhledem k b 1 a dostaneme systém: b 1, b 2, a 3,…, a n (4)

Podle ortogonalizačních kroků je systém (4) lineárně nezávislý a jeho část b 1, b 2- ortogonální.

Předpokládejme, že lineárně nezávislý systém již byl zkonstruován b 1, b 2, …, b k-1, a k,…, a n, (5)

ve kterém b 1, b 2, …, b k-1– ortogonální.

V k-tém kroku k = 3, n nahradíme vektor v systému (5) a k jeho ortogonální složku vzhledem k systému b 1, b 2, …, b k-1 a dostaneme systém b 1 , …, b k , a k+1 , …, a n.

Po dokončení n-tého kroku získáme lineárně nezávislý a ortogonální systém vektorů b 1, b 2, …, b n.

Vstupenka 20.Uveďte definici operátoru v lineárním prostoru. Který operátor se nazývá lineární.

Operátor je pravidlo, podle kterého každý prvek X X je spárován jeden prvek y nějaká neprázdná sada Y . Operátor prý jedná od X PROTI Y .

Akce operátora je označena y = A (X), y- obraz X, X- prototyp y.

Pokud každý prvek y z Y má jediný prototyp X z X , y= A (X), volá se operátor mapování jedna ku jedné X PROTI Y nebo transformace X , X - rozsah definice operátora.

Nechat X A Y dva lineární prostory. Operátor A , působící od X PROTI Y , volal lineární operátor, pokud pro jakékoli dva prvky u A proti z X a libovolné číslo α platí:

A(u+ proti) = A (u) + A (proti) , A (α· u) = α· A (u).

Vstupenka 21. Uveďte příklad lineárního operátoru. Jaké operace na lineárních operátorech znáte?

ÚHEL MEZI ROVINAMI

Uvažujme dvě roviny α 1 a α 2 definované rovnicemi:

Pod úhel mezi dvěma rovinami budeme rozumět jednomu z dihedrálních úhlů tvořených těmito rovinami. Je zřejmé, že úhel mezi normálovými vektory a rovinami α 1 a α 2 je roven jednomu z naznačených sousedních dihedrálních úhlů popř. . Proto . Protože A , Že

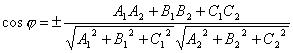Příklad. Určete úhel mezi rovinami X+2y-3z+4=0 a 2 X+3y+z+8=0.

Podmínka pro rovnoběžnost dvou rovin.

Dvě roviny α 1 a α 2 jsou rovnoběžné právě tehdy, když jsou jejich normálové vektory rovnoběžné, a proto .

Dvě roviny jsou tedy navzájem rovnoběžné právě tehdy, když koeficienty odpovídajících souřadnic jsou úměrné:

nebo

Podmínka kolmosti rovin.

Je jasné, že dvě roviny jsou kolmé právě tehdy, když jsou jejich normálové vektory kolmé, a proto, nebo .

Tím pádem, .

Příklady.

PŘÍMO V PROSTORU.

VEKTOROVÁ ROVNICE PRO ČÁRU.

PARAMETRICKÉ PŘÍMÉ ROVNICE

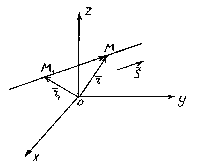
Poloha čáry v prostoru je zcela určena určením libovolného z jejích pevných bodů M 1 a vektor rovnoběžný s touto přímkou.

Vektor rovnoběžný s přímkou se nazývá průvodci vektor této čáry.

Nechte tedy rovnou čáru l prochází bodem M 1 (X 1 , y 1 , z 1), ležící na přímce rovnoběžné s vektorem .

Zvažte libovolný bod M(x,y,z) na přímce. Z obrázku je zřejmé, že .

Vektory a jsou kolineární, takže existuje takové číslo t, co , kde je násobitel t může nabývat libovolné číselné hodnoty v závislosti na poloze bodu M na přímce. Faktor t nazývaný parametr. Po určení poloměrových vektorů bodů M 1 a M respektive prostřednictvím a , získáme . Tato rovnice se nazývá vektor rovnice přímky. Ukazuje, že pro každý parametr hodnotu t odpovídá vektoru poloměru nějakého bodu M, ležící na přímce.

Zapišme tuto rovnici v souřadnicovém tvaru. Všimněte si, že, a odtud

Výsledné rovnice se nazývají parametrické rovnice přímky.

Při změně parametru t změna souřadnic X, y A z a tečka M se pohybuje v přímé linii.

KANONICKÉ ROVNICE PŘÍMÉ

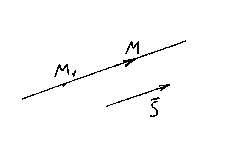
Nechat M 1 (X 1 , y 1 , z 1) – bod ležící na přímce l, A je jeho směrový vektor. Vezměme opět libovolný bod na přímce M(x,y,z) a zvažte vektor .

Je jasné, že vektory jsou také kolineární, takže jejich odpovídající souřadnice musí být úměrné,

– kanonický rovnice přímky.

Poznámka 1. Všimněte si, že kanonické rovnice přímky lze získat z parametrických eliminací parametru t. Ve skutečnosti z parametrických rovnic, které získáme nebo .

Příklad. Zapište rovnici přímky v parametrické podobě.

Označme , odtud X = 2 + 3t, y = –1 + 2t, z = 1 –t.

Poznámka 2 Nechť je přímka kolmá k jedné ze souřadnicových os, například k ose Vůl. Potom je směrový vektor přímky kolmý Vůl, tedy, m=0. V důsledku toho budou mít parametrické rovnice přímky tvar

Vyloučení parametru z rovnic t, získáme rovnice přímky ve tvaru

I v tomto případě však souhlasíme s formálním zápisem kanonických rovnic přímky do formuláře . Pokud je tedy jmenovatel jednoho ze zlomků nulový, znamená to, že přímka je kolmá k příslušné souřadnicové ose.

Podobně jako u kanonických rovnic odpovídá přímce kolmé k osám Vůl A Oj nebo rovnoběžně s osou Oz.

Příklady.

OBECNÉ ROVNICE PŘÍMKY JAKO ČÁRY KŘÍŽENÍ DVOU ROVIN

Obecně jakékoli dvě nerovnoběžné roviny dané obecnými rovnicemi

určit přímku jejich průsečíku. Tyto rovnice se nazývají obecné rovnice rovný.

Příklady.

Sestrojte přímku danou rovnicí

K sestrojení přímky stačí najít dva její body. Nejjednodušší způsob je vybrat průsečíky přímky se souřadnicovými rovinami. Například průsečík s rovinou xOy získáme z rovnic přímky za předpokladu z= 0:

Po vyřešení tohoto systému najdeme pointu M 1 (1;2;0).

Podobně za předpokladu y= 0, dostaneme průsečík přímky s rovinou xOz:

Od obecných rovnic přímky lze přejít k jejím kanonickým nebo parametrickým rovnicím. Chcete-li to provést, musíte najít nějaký bod M 1 na přímce a směrový vektor přímky.

Souřadnice bodu M 1 získáme z tohoto systému rovnic, přičemž jedné ze souřadnic přiřadíme libovolnou hodnotu. Chcete-li najít směrový vektor, poznamenejte si, že tento vektor musí být kolmý k oběma normálovým vektorům A . Tedy mimo směrový vektor přímky l můžete vzít vektorový součin normálních vektorů:

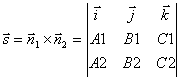Příklad. Uveďte obecné rovnice přímky na kanonickou formu.

Najdeme bod ležící na přímce. K tomu zvolíme libovolně jednu ze souřadnic, např. y= 0 a vyřeš soustavu rovnic:

Normální vektory rovin definujících přímku mají souřadnice Proto bude směrový vektor přímý

. Proto, l: .

ÚHEL MEZI PŘÍMKAMI

Úhel mezi přímkami v prostoru budeme nazývat libovolný ze sousedních úhlů tvořených dvěma přímkami vedenými libovolným bodem rovnoběžným s daty.

Nechť jsou v prostoru uvedeny dvě čáry:

Je zřejmé, že úhel φ mezi přímkami lze brát jako úhel mezi jejich směrovými vektory a . Od , pak pomocí vzorce pro kosinus úhlu mezi vektory dostaneme

Úkol vyžaduje najděte průsečík dvou rovin a určete skutečnou velikost jedné z nich metodou planparalelního pohybu.

Chcete-li vyřešit takový klasický problém v deskriptivní geometrii, musíte znát následující teoretický materiál:

— kreslení projekcí vesmírných bodů na komplexní výkres na daných souřadnicích;

— metody pro specifikaci roviny ve složitém výkresu, obecné a konkrétní roviny;

— hlavní linie letadla;

— určení průsečíku přímky s rovinou (zjištění "místa setkání");

— metoda planparalelního pohybu pro určení přirozené velikosti ploché postavy;

— určení viditelnosti přímek a rovin ve výkresu pomocí konkurenčních bodů.

Postup při řešení Problému

1. Podle volby Přiřazení pomocí souřadnic bodů vykreslíme na složitý výkres dvě roviny, zadané ve tvaru trojúhelníků ABC(A', B', C'; A, B, C) a DKE(D', K', E'; D, K, E) ( Obr.1.1).

Obr.1.1

2 . K nalezení průsečíku používáme metoda promítací roviny. Jeho podstatou je, že jedna strana (přímka) první roviny (trojúhelník) je vzata a uzavřena v promítací rovině. Určí se průsečík této přímky s rovinou druhého trojúhelníku. Opakováním tohoto úkolu znovu, ale pro přímku druhého trojúhelníku a rovinu prvního trojúhelníku určíme druhý průsečík. Protože výsledné body patří současně do obou rovin, musí být na průsečíku těchto rovin. Spojením těchto bodů přímkou získáme požadovanou linii průsečíku rovin.

3. Problém je vyřešen následovně:

A) uzavřít v projekční rovině F(F') boční AB(A’ B’) první trojúhelník ve frontální rovině průmětů PROTI. Vyznačíme průsečíky promítací roviny se stranami DK A DE druhý trojúhelník, získávání bodů 1(1') a 2 (2'). Přeneseme je po komunikačních liniích do vodorovné promítací roviny H na odpovídající strany trojúhelníku, bod 1 (1) na straně DE a tečka 2(2) na straně DK.

Obr.1.2

b) spojující průměty bodů 1 a 2, budeme mít průmět promítací roviny F. Potom průsečík přímky AB s rovinou trojúhelníku je určena DKE (podle pravidla) spolu s průsečíkem průmětu promítací roviny. 1-2 a promítání stejnojmenné čáry AB. Tak jsme získali vodorovný průmět prvního průsečíku rovin - M, kterým určujeme (promítáme po komunikačních liniích) jeho čelní průmět – M’ na přímce A’ B’ (Obr.1.2.a);

PROTI) druhý bod najdeme podobným způsobem. Uzavřeme ji do promítací roviny G(G) straně druhého trojúhelníku DK(DK) . Označíme průsečíky promítací roviny se stranami prvního trojúhelníku A.C.APŘED NAŠÍM LETOPOČTEM. ve vodorovném promítání, získávání průmětů bodů 3 a 4. Promítneme je na odpovídající strany ve frontální rovině, dostaneme 3’ a 4'. Jejich spojením přímkou máme průmět promítací roviny. Potom bude druhý průsečík rovin v průsečíku přímky 3’-4’ se stranou trojúhelníku D’ K’ , který byl uzavřen v projekční rovině. Tak jsme získali čelní průmět druhého průsečíku - N’ , podél komunikační linie najdeme horizontální projekci - N (Obr.1.2.b).

G) spojující výsledné body MN(MN) A (M’ N’) na vodorovné a čelní rovině máme požadovanou průsečík daných rovin.

4. Pomocí konkurenčních bodů určujeme viditelnost rovin. Vezměme si pár konkurenčních bodů, např. 1’=5’ ve frontální projekci. Promítneme je na odpovídající strany do vodorovné roviny a dostaneme 1 a 5. V tom vidíme smysl 1 , ležící na boku DE má velkou souřadnici k ose X než bod 5 , ležící na boku AV. Proto podle pravidla čím větší souřadnice, tím bod 1 a strana trojúhelníku D'E“ ve frontální rovině bude vidět. Tak je určena viditelnost každé strany trojúhelníku v horizontální a čelní rovině. Viditelné čáry ve výkresech jsou nakresleny jako plná obrysová čára a neviditelné čáry jsou nakresleny jako přerušovaná čára. Připomeňme, že v průsečících rovin ( M— N AM’- N’ ) dojde ke změně viditelnosti.

Obr.1.3

RObr. 1.4 .

Diagram navíc ukazuje určení viditelnosti ve vodorovné rovině pomocí konkurenčních bodů 3 A 6 na přímkách DK A AB.

5. Metodou planparalelního pohybu určíme přirozenou velikost roviny trojúhelníku ABC, Proč:

A) v zadané rovině přes bod C(C) provést čelní C— F(S-FAC’- F’) ;

b) na volném poli výkresu ve vodorovném promítání vezmeme (označíme) libovolný bod C 1, uvážíme-li, že se jedná o jeden z vrcholů trojúhelníku (konkrétně vrchol C). Z ní obnovíme kolmici na frontální rovinu (průchozí osa x);

Obr.1.5

PROTI) planparalelním pohybem převádíme horizontální průmět trojúhelníku ABC, na novou pozici A 1 B 1 C 1 tak, že ve frontální projekci zaujme vyčnívající polohu (přemění se v přímku). K tomu: na kolmici z bodu C 1, odložte čelní horizontální projekci C 1 — F 1 (délka l CF) získáváme bod F 1 . Řešení kompasu z bodu F 1 velikost F-A uděláme obloukový zářez a od bodu C 1 - velikost zářezu C.A., pak v průsečíku obloukových čar dostaneme bod A 1 (druhý vrchol trojúhelníku);

- podobně dostaneme pointu B 1 (z bodu C 1 udělat zářez velikosti C— B(57 mm) a od bodu F 1 velikost F— B(90 mm) Všimněte si, že správné řešení má tři body A 1 F’ 1 A B’ 1 musí ležet na stejné přímce (strana trojúhelníku A 1 — B 1 ) dvě další strany S 1 — A 1 A C 1 — B 1 jsou získány spojením jejich vrcholů;

G) z metody rotace vyplývá, že při pohybu nebo otáčení bodu v nějaké promítací rovině - na sdružené rovině se průmět tohoto bodu musí pohybovat po přímce, v našem konkrétním případě po přímé rovnoběžné ose. X. Poté losujeme z bodů A’ B’ C’ z čelní projekce tyto přímky (nazývají se rovinami rotace bodů) a z čelních průmětů posunutých bodů A 1 V 1C 1 obnovit kolmice (spojovací čáry) ( Obr.1.6).

Obr.1.6

Průsečík těchto přímek s odpovídajícími kolmicemi dává nové polohy čelního průmětu trojúhelníku ABC, konkrétně A’ 1 V 1C’ 1 která by se měla stát projektivní (přímka), protože horizontální h 1 kreslili jsme kolmo k frontální rovině projekcí ( Obr.1.6);

5) pak pro získání přirozené velikosti trojúhelníku stačí otočit jeho čelní průmět, dokud není rovnoběžný s vodorovnou rovinou. Otáčení se provádí pomocí kompasu přes bod A' 1, považujeme jej za střed otáčení, umístíme trojúhelník A’ 1 V 1C’ 1 rovnoběžně s osou X, dostaneme A’ 2 AT 2C’ 2 . Jak bylo uvedeno výše, když se bod otáčí, na konjugované (nyní horizontální) projekci se pohybují po přímých liniích rovnoběžných s osou X. Vynechání kolmiček (spojovacích čar) z čelních průmětů bodů A’ 2 AT 2C’ 2 jejich křížením s odpovídajícími čarami najdeme vodorovný průmět trojúhelníku ABC (A 2 AT 2C 2 ) skutečná velikost ( Obr.1.7).

Rýže. 1.7

Mám všechna hotová řešení problémů s takovými souřadnicemi, můžete si je koupit

Cena 55 rublů., výkresy deskriptivní geometrie z Frolovovy knihy si můžete snadno stáhnout ihned po zaplacení nebo vám je pošlu na email. Jsou v archivu ZIP v různých formátech:
*.jpg – běžná barevná kresba kresby v měřítku 1 až 1 v dobrém rozlišení 300 dpi;
*.cdw – Formát programu Compass 12 a vyšší nebo verze LT;
*.dwg a .dxf — AUTOCAD, formát programu nanoCAD;

Sekce: Deskriptivní geometrie /

Přímku v prostoru lze definovat jako průsečík dvou nerovnoběžných rovin, tedy jako množinu bodů splňujících systém dvou lineárních rovnic.

(V.5)

Platí i obrácené tvrzení: soustava dvou nezávislých lineárních rovnic tvaru (V.5) definuje přímku jako průsečík rovin (pokud nejsou rovnoběžné). Jsou volány rovnice soustavy (V.5). obecná rovnice přímka v prostoru
.

PříkladPROTI.12 . Sestavte kanonickou rovnici přímky dané obecnými rovnicemi rovin

Řešení. Chcete-li napsat kanonickou rovnici přímky nebo, což je totéž, rovnici přímky procházející dvěma danými body, musíte najít souřadnice libovolných dvou bodů na přímce. Mohou to být například průsečíky přímky s libovolnými dvěma rovinami souřadnic Oyz A Oxz.

Průsečík přímky a roviny Oyz má úsečku
. Tedy za předpokladu v této soustavě rovnic
, dostaneme systém se dvěma proměnnými:

Její rozhodnutí
,
dohromady s
definuje bod
požadovanou přímku. Za předpokladu v této soustavě rovnic
, dostaneme systém

jehož řešení
,
dohromady s
definuje bod
průsečík přímky s rovinou Oxz.

Nyní si zapišme rovnice přímky procházející body
A
:
nebo
, Kde
bude směrový vektor této přímky.

PříkladPROTI.13. Přímka je dána kanonickou rovnicí
. Napište obecnou rovnici pro tento řádek.

Řešení. Kanonická rovnice přímky může být zapsána jako systém dvou nezávislých rovnic:



Získali jsme obecnou rovnici přímky, která je nyní dána průsečíkem dvou rovin, z nichž jedna je
rovnoběžně s osou Oz (
), a ostatní
- sekery OU (
).

Tato přímka může být reprezentována jako průsečík dvou dalších rovin napsáním její kanonické rovnice ve formě další dvojice nezávislých rovnic:



Komentář . Stejná přímka může být definována různými systémy dvou lineárních rovnic (tedy průsečíkem různých rovin, protože jednou přímkou lze nakreslit nekonečné množství rovin), a také různými kanonickými rovnicemi (v závislosti na volba bodu na přímce a její směrový vektor) .

Nenulový vektor rovnoběžný s přímkou, budeme mu říkat vodicí vektor .

Vpusťte do trojrozměrného prostoru je dána přímka l, procházející bodem
a jeho směrový vektor
.

Jakýkoli vektor
, Kde
, ležící na čáře, je kolineární s vektorem , proto jsou jejich souřadnice úměrné, tzn

. (V.6)

Tato rovnice se nazývá kanonická rovnice přímky. Ve speciálním případě, kdy ﻉ je rovina, dostaneme rovnici přímky na rovině

. (V.7)

PříkladPROTI.14. Najděte rovnici přímky procházející dvěma body
,
.

Kde
,
,
.

Rovnici (V.6) je vhodné psát v parametrickém tvaru. Protože souřadnice směrových vektorů rovnoběžných čar jsou úměrné, pak za předpokladu

Kde t - parametr,
.

Vzdálenost od bodu k řádku

Uvažujme dvourozměrný euklidovský prostor ﻉ s kartézským systémem souřadnic. Nechte bod
ﻉ a lﻉ. Pojďme najít vzdálenost od tohoto bodu k přímce. Položme
a rovnou l daný rovnicí
(obr.V.8).

Vzdálenost
, vektor
, Kde
– vektor normální čáry l,
A – kolineární, takže jejich souřadnice jsou úměrné, tzn
, tedy,
,
.

Odtud
nebo vynásobením těchto rovnic A A B a jejich přidáním najdeme
, odtud

(V.8)

určuje vzdálenost od bodu
na přímku
.

PříkladPROTI.15. Najděte rovnici přímky procházející bodem
kolmo k přímce l:
a najít vzdálenost od
na přímku l.

Z Obr. V.8 máme
a normální vektor je rovný l
. Z podmínky kolmosti, kterou máme

Protože
, Že

. (V.9)

Toto je rovnice přímky procházející bodem
,kolmo k přímce
.

Mějme rovnici přímky (V.9) procházející bodem
, kolmo na čáru l:
. Najděte vzdálenost od bodu
na přímku l pomocí vzorce (V.8).

Pro zjištění požadované vzdálenosti stačí najít rovnici přímky procházející dvěma body
a tečka
ležící na čáře na základně kolmice. Nechat
, Pak

Protože
a vektor
, Že

. (V.11)

Od věci
leží na přímce l, pak máme další rovnost
nebo

Zredukujeme systém do podoby vhodné pro aplikaci Cramerovy metody

Jeho řešení má tvar

. (V.12)

Dosazením (V.12) do (V.10) získáme původní vzdálenost.

PříkladPROTI.16. Bod je dán ve dvourozměrném prostoru
a rovný
. Najděte vzdálenost od bodu
na přímku; napište rovnici přímky procházející bodem
kolmo k dané přímce a zjistěte vzdálenost od bodu
k základně kolmice k původní přímce.

Podle vzorce (V.8) máme

Rovnici přímky obsahující kolmici najdeme jako přímku procházející dvěma body
A
za použití vzorce (V.11). Protože
, tedy s přihlédnutím ke skutečnosti, že
, A
, my máme

Chcete-li zjistit souřadnice
máme systém zohledňující skutečnost, že bod
leží na původní čáře

Proto,
,
, odtud.

Uvažujme trojrozměrný euklidovský prostor ﻉ. Nechte bod
ﻉ a rovina ﻉ. Pojďme najít vzdálenost od tohoto bodu
do roviny  dané rovnicí (obr. V.9).

Podobně jako my máme dvourozměrný prostor
a vektor
, ah, odtud

. (V.13)

Rovnici přímky obsahující kolmici k rovině  zapíšeme jako rovnici přímky procházející dvěma body
A
, ležící v letadle:

. (V.14)

Chcete-li zjistit souřadnice bodu
k libovolným dvěma rovnostem vzorce (V.14) přidáme rovnici

Řešením soustavy tří rovnic (V.14), (V.15) najdeme ,,– souřadnice bodu
. Poté bude rovnice kolmice zapsána ve tvaru

Chcete-li zjistit vzdálenost od bodu
do roviny místo vzorce (V.13) použijeme

Vpusťte kanonické rovnice přímky

koeficient je odlišný od nuly, tj. přímka není rovnoběžná s rovinou xOy. Zapišme tyto rovnice samostatně v tomto tvaru:

Za našich podmínek rovnice (6) zcela definují přímku. Každý z nich jednotlivě vyjadřuje rovinu, přičemž první z nich je rovnoběžný s osou Oy a druhý s osou

Tedy představující přímku s rovnicemi tvaru (6) ji považujeme za průsečík dvou rovin, které tuto přímku promítají na souřadnicovou rovinu xOz a yOz. První z rovnic (6), uvažovaná v rovině, určuje průmět dané přímky do této roviny; stejně tak druhá z rovnic (6), uvažovaná v rovině, určuje průmět dané přímky na rovinu yOz. Dá se tedy říci, že dát rovnici přímky ve tvaru (6) znamená dát její průmět na souřadnicovou rovinu xOz a yOz.

Pokud by byl vodící koeficient nulový, pak by se alespoň jeden z dalších dvou koeficientů například lišil od nuly, tj. přímka by nebyla rovnoběžná s rovinou yOz. V tomto případě bychom mohli vyjádřit přímku

rovnice rovin promítnou to do souřadnicových rovin zápisem rovnic (5) do formuláře

Jakákoli přímka tedy může být vyjádřena rovnicemi dvou rovin, které jí procházejí a promítají ji do souřadnicových rovin. Ale není vůbec nutné definovat přímku právě takovou dvojicí rovin.

Každou přímkou prochází nespočet rovin. Jakékoli dva z nich, které se protínají, jej definují v prostoru. V důsledku toho rovnice jakýchkoli dvou takových rovin, uvažované společně, představují rovnice této přímky.

Obecně platí, že jakékoli dvě roviny, které nejsou vzájemně rovnoběžné s obecnými rovnicemi

určit přímku jejich průsečíku.

Rovnice (7), uvažované společně, se nazývají obecné rovnice přímky.

Z obecných rovnic přímky (7) můžeme přejít k jejím kanonickým rovnicím. Pro tento účel musíme znát nějaký bod na přímce a směrový vektor.

Souřadnice bodu z dané soustavy rovnic snadno zjistíme tak, že si libovolně vybereme jednu ze souřadnic a poté vyřešíme soustavu dvou rovnic pomocí členů zbývajících dvou souřadnic.

Abychom našli směrový vektor přímky, všimneme si, že tento vektor směrovaný podél průsečíku těchto rovin musí být kolmý k oběma normálovým vektorům těchto rovin. Naopak každý vektor kolmý k je rovnoběžný s oběma rovinami, a tedy s danou přímkou.

Tuto vlastnost má ale i vektorový součin. Proto vektorový součin normálových vektorů těchto rovin lze brát jako směrovací vektor přímky.

Příklad 1. Redukujte rovnici přímky na kanonickou formu

Zvolme si libovolně jednu ze souřadnic. Nechť například . Pak

odkud jsme tedy našli bod (2, 0, 1) ležící na přímce,

Když nyní najdeme vektorový součin vektorů, získáme směrový vektor přímky. Kanonické rovnice tedy budou:

Komentář. Od obecných přímkových rovnic ve tvaru (7) můžete přejít ke kanonickým, aniž byste se uchýlili k vektorové metodě.

Zastavme se nejprve trochu podrobněji u rovnic

Vyjádřeme z nich x a y prostřednictvím . Pak dostaneme:

kde by to mělo být

Rovnice (6) se v průmětech na rovinu nazývají přímkové rovnice

Stanovme si geometrický význam konstant M a N: M je úhlový koeficient průmětu dané přímky do souřadnicové roviny (tangens úhlu tohoto průmětu s osou Oz) a N je úhlový koeficient. průmětu této přímky do souřadnicové roviny (tangens úhlu tohoto průmětu s osou Oz). Čísla tedy určují směry průmětů dané přímky do dvou souřadnicových rovin, tedy charakterizují i samotný směr dané přímky. Proto se číslům M a N říká úhlové koeficienty dané úsečky.

Abychom zjistili geometrický význam konstant, dáme do rovnic (6) přímku, pak dostaneme: to znamená, že bod leží na dané přímce. Je zřejmé, že tento bod je průsečíkem této přímky s rovinou. Toto jsou tedy souřadnice stopy této přímky na souřadnicové rovině

Nyní je snadné provést přechod od projekčních rovnic ke kanonickým. Uveďme například rovnice (6). Řešením těchto rovnic pro , zjistíme: